Теорема Карно

Энергии в работу.

Основные теоретические представления о превращении теплоты в работу были сформулированы С. Карно в 1824 году. Карно рассмотрел идеальный тепловой двигатель, работающий по циклу, который впоследствии получил название цикла Карно, и сформулировал основные положения, лежащие в основе работы тепловых двигателей. Для осуществления теплового двигателя необходимо иметь, по крайней мере, два тепловых резервуара с различными температурами T₁ и T₂ (см. рис. 2.1.1). Сжатие и расширение рабочего тела должно происходить при разных температурах, так как только в этом случае будет совершена положительная (полезная) работа. Рабочее тело двигателя, приведенное в контакт с горячим источником теплоты, начинает расширяться. Чтобы процесс расширения был обратимым, необходимо равенство температур тела и резервуара при расширении, которое имеет место только тогда, когда расширение происходит достаточно медленно. Та же ситуация имеет место и при сжатии. От горячего источника теплоты с температурой Т₁ в процессе расширения берется тепло q₁. В процессе сжатия холодному источнику теплоты с температурой Т₂ отдается тепло q₂. Чтобы замкнуть цикл, нужно изолировать на время перехода вещество от обоих резервуаров и заставить менять свое состояние по адиабатам (см. рис. 2.1.1). За цикл рабочее тело совершит работу l=q₁-q_2. Термический коэффициент полезного действия (КПД) теплового двигателя

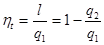
В качестве примера рабочего тела, совершающего цикл Карно, Р. Клаузиус взял идеальный газ и провел расчет КПД цикла. В состоянии 1 температура газа равна температуре Т₁ горячего источника теплоты. В процессе изотермического расширения газ переходит в состояние 2 (процесс 1-2 на рис. 2.1.2). Совершаемая газом удельная работа

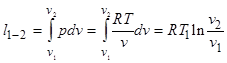. (2.1.1) Внутренняя энергия идеального газа зависиттолькоот температуры и при изотермическом расширении не изменяется. Следовательно, согласно первому законутермодинамики тепло, полученное от горячего источника q ₁= l _1-2. Из состояния 2 в состояние 3 газ переходит, расширяясь по адиабате и совершая работу. Согласно первому закону термодинамики эта работа равно убыли его внутренней энергии

.

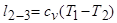В процессе 3-4 изотермического сжатия совершаемая газом работа

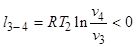, (2.1.2)

т.к. движение поршня происходит против действия силы давления. Сжатие газа требует затрат энергии от внешнего источника, которым служит, используемый в машине, маховик. Отдаваемое газом тепло q₂>0 холодному источнику q ₂=- l _3-4. Работа, совершаемая газом при адиабатическом сжатии

.

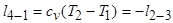Суммарная работа, совершенная газом за цикл,

l = l _1-2 + l _2-3 + l _3-4 + l _4-1 = l _1-2 + l _3-4 (2.1.3)

Преобразуем полученное выражение, воспользовавшись формулой для адиабаты. Из нее следует, что

.

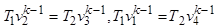Если теперь разделить по-членно первую формулу на вторую, то получим, что

.

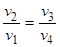Суммарная работа, совершенная газом, как следует из формул (2.1.1) -(2.1.3) оказывается равной

,

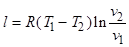а термический КПД

. (2.1.4)

Формула (2.1.4) известна как формула Карно.

Приведенный вывод исходил из предположения, что рабочим телом служит идеальный газ. В действительности она справедлива для любого рабочего тела, совершающего обратимый цикл Карно.

Сформулируем положение, известное как теорема Карно. Пусть рабочее тело совершает цикл Карно (см. рис.2.1.2). Отношение количества тепла q₁, полученного от горячего источника тепла, к количеству тепла q₂ , отданного холодному источнику тепла, не зависит от природы рабочего тела и определяется только температурой T₁ нагревателя и температурой холодильника T ₂ :

. (2.1.5)

Иными словами, (см. формулу (2.2.1)) термический коэффициент полезного действия любой машины, работающей по обратимому циклу Карно не зависит от природы рабочего тела, а определяется только температурами горячего и холодного источников тепла.

Р.Клаузиус дал доказательство этой теоремы, исходя из следующего положения: теплота не может переходить сама собой от более холодного тела к более горячему.

Отсутствие самопроизвольного перехода тепла вовсе не означает, что нельзя осуществить передачу тепла от холодного тела к горячему. Однако, для того, чтобы это произошло нужно, затратить работу внешних сил по отношению к рассматриваемой термодинамической системе. Без внешнего воздействия такой переход невозможен. Это положение легло в основу одной из формулировок второго начала термодинамики.

Рассмотрим это доказательство. Пусть имеются два рабочих тела C и C'. Предположим, что они берут одинаковое количество тепла q₁ = q₁ ' из горячего источника К₁ тепла и передают разные количества q₂ < q₂' холодному источнику К₂. Заставим первое тело совершить цикл Карно и передать источнику К₂ тепло q₂. Второе тело заставим проделать круговой процесс в обратном направлении. Оно возьмет тепло q₂' из холодного источника К₂ и вернет источнику К₁ тепло q₁, взятое первым телом. Так как первое тело совершило большую работу, чем нужно затратить второму для возвращения тела источнику К₁, то есть избыток работы Dl = l - l' > 0. Таким образом, нам удалось получить работу за счет тепла одного источника. Эту работу всегда можно потратить на передачу тепла от холодного тела к горячему. В результате в системе из двух источников тепла и двух машин осуществился переход тепла от холодного источника тепла к горячему без затрат работы со стороны внешних к системе тел. Остается одно, что q₂ = q₂'.

Из формулы (2.1.4), найденной для идеального газа, немедленно следует, что для любого тела, совершающего цикл Карно,

,

или

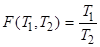. (2.1.6)

Таким образом, второе начало термодинамики позволяет определить вид функции F(T₁,T₂).

В расчетах удобно говорить только о поглощаемой теплоте и рассматривать отдаваемое количество теплоты как поглощаемое со знаком минус. Принимая такое правило знаков, запишем полученный результат в виде

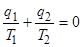. (2.1.7)

Формулу (2.1.7) легко обобщить на произвольный циклический процесс, представив его как совокупность большого числа циклов Карно, к каждому из которых применимо равенство (2.1.6). В результате получим

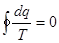. (2.1.8)

Формула (2.1.8) позволяет определить энтропию равенством

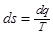(2.1.9)

для любого тела.

Существуют другие формулировки второго закона термодинамики. Одна из них была дана В. Томсоном в 1851 году: периодически действующая машина, единственным результатом действия которой было бы производство работы за счет получения тепла от одного источника, невозможна. Другая формулировка состоит в невозможности вечного двигателя второго рода, способного совершать работу за счет тепла одного источника. Все эти формулировки второго закона термодинамики эквивалентны и из одной из них немедленно следует другая.

Дата добавления: 2015-06-27