Энтропия как физическая характеристика преобразования тепла в работу. Неравенство Клаузиуса

Формальное определение энтропии основано на формуле (2.1.8), которая в свою очередь следует из второго начала термодинамики. Физический смысл энтропии виден из неравенства, выведенного Р. Клаузиусом.

Рассмотрим этот вывод. Пусть имеется два тепловых резервуара R₁ , R₂ с температурами T₁, T₂ соответственно. Тепловая машина берет из резервуара R₁ тепло Q₁ (Q₁> 0) и передает резервуару R₂ тепло Q₂ (Q₂ <0), совершая работу

L = Q₁ + Q₂.

Возьмем теперь вторую тепловую машину, работающую по обратимому циклу Карно так, что она берет из резервуара R₂ тепло Q’₂ (Q’₂ >0) и отдает резервуару R₁ тепло Q’₁ <0. Работа совершенная машиной

L’ = Q’₁ + Q’₂

отрицательна, т.к. на ее привод затрачивается работа, совершенная внешними телами. Пусть вторая машина возвращает резервуару R₁ тепло, взятое первой машиной, т.е. Q’₁ = -Q₁, тогда суммарная работа двух машин

L = Q₁ + Q₂ + Q’₁ + Q’₂ £ 0 (2.1.10)

может быть только отрицательной. В противном случае получается устройство, способное производить работу за счет тепла, взятого только у одного резервуара R₂. что невозможно.

Для машины, работающей по обратимому циклу Карно

Q’₁/T₁ + Q’₂/T₂ = 0,

откуда

Q’₂ =-Q’₁ T₂/T₁ = Q₁ T₂/T₁. (2.1.11)

Подставляя (2.1.11) в (2.1.10), получим неравенство

Q₁/T₁ + Q₂/T₂ £ 0, (2.1.12)

называемое неравенством Клаузиуса. Из формулы следует, что за один цикл приведенное количество тепла, полученное рабочим телом от горячего источника тепла по величине меньше или равно приведенному теплу, отданному холодному источнику, и эти величины равны только для обратимого процесса. Горячий источник тепла не изменяет своей температуры при отборе тепла рабочим телом, его энтропия уменьшается на величину приведенного тепла за один цикл (см. формулу (2.1.9)). Соответственно увеличивается энтропия холодного источника тепла. Суммарное изменение энтропии системы из двух резервуаров и рабочего тела машины за цикл, как следует из неравенства (2.1.12), происходит в сторону увеличения. Энтропия холодного источника растет быстрее, чем уменьшается энтропия горячего. Иными словами, реальные физические процессы в тепловых машинах всегда сопровождаются ростом энтропии системы.

Неравенство (2.1.12) имеет ряд обобщений и следствий. Рассмотрим одно из них. Термический КПД тепловой машины определяется формулой

h = 1 - Q₂ /Q₁,

если считать Q₂ положительным. Из неравенства (2.1.12) следует, что

h £ 1 - T₂ /T₁.

Следовательно, коэффициент полезного действия любой тепловой машины не может превосходить коэффициента полезного действия идеальной тепловой машины, работающей по циклу Карно с теми же температурами нагревателя и холодильника.

Неравенство (2.1.12) допускает обобщение на ряд с произвольным

числом n тепловых резервуаров R₁,R₂,...R_n с температурами T_1,,T₂,...T_n

S Q_i/T_i £ 0. (2.1.13)

ⁱ

Если температура меняется непрерывно, то процесс осуществляется припомощи непрерывного ряда тепловых резервуаров. Из каждого система поглощает некоторое количество тепла dQ. Неравенство

(2.1.13) принимает вид

. (2.1.14)

Пусть система переходит из состояния 1 в 2, а затем обратно из 2 в 1 в

результате обратимого процесса, тогда

.

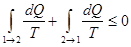Второй интеграл выражается через приращение энтропии

,

и в результате неравенство Клаузиуса принимает вид:

.

В частности, когда состояние 2 бесконечно близко к состоянию 1,

или

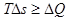. (2.1.15)

Изменение энтропии не меньше полученного приведенного количества тепла.

2.1.3. Свободная энергия.

Работа L, совершаемая замкнутой термодинамической системой, равна убыли ее внутренней энергии:

L = - DU. (2.1.16)

Равенство не справедливо в общем случае для произвольной термодинамической системы, т.к. всегда происходит обмен энергией с окружающей средой. Предположим, что температура Т окружающей среды остается постоянной при переход системы из состояния 1 в состояние 2. В силу неравенства Клаузиуса

,

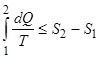или, вынося постоянный множитель из под знака интеграла, найдем

. (2.1.17)

Формула (2.1.17) устанавливает верхний предел количества тепла, которое система получает от окружающей среды в процессе 1-2. Работа, совершенная системой, согласно первому закону термодинамики

L= -DU + Q £ - U₂ + U₁ + T(S₂ - S₁)£ -F₂ + F₁ = -DF, (2.1.18)

где

F = U - TS. (2.1.19)

Функция F называется свободной энергией системы. Если процесс обратим, то температура системы равна температуре окружающей среды, и в формуле (2.1.18) стоит знак равенства. В этом случае совершенная работа равна своему верхнему пределу. Иными словами, совершенная работа никогда не может быть больше убыли свободной энергии системы и достигает своего максимального значения для обратимых процессов. Этим собственно и объясняется принятое название функции F. Эта та часть внутренней энергии системы, которая может быть использована для получения работы.

2.1.4. Термодинамический потенциал Гиббса.

Рассмотрим термодинамическую систему, которая при постоянной температуре T и постоянном давлении p совершает переход из состояния 1 с объемом V₁ в состояние 2 с объемом V₂. В качестве такой системы можно, например, взять цилиндр с жидкостью и насыщенным паром или любую другую систему, состояние которой не определяется однозначно давлением и температурой, как у простой однородной системы. При переходе 1-2 система совершает работу

.

Так как переход происходит при постоянной температуре, то к нему применимо неравенство (3.7.3):

,

или, если определить функцию состояния

G = F + pV, (2.1.20)

которая называется термодинамическим потенциалом Гиббса, то

G₁ ³ G₂. (2.1.21)

Из формулы (2.1.21) следует, что при изобарическом переходе системы из состояния 1 в состояние 2 ее термодинамический потенциал не может увеличиваться. Если термодинамический потенциал при данном давлении и температуре минимален, то система находится в состоянии устойчивого равновесия. Действительно, всякое изменение состояния привело бы, согласно (2.1.21) к уменьшению G, что противоречит условию минимума G.

В тепловых машинах система при переходе из состояния 1 в состояние 2 совершает работу не только против сил внешнего давления, но еще и полезную работу L'. К суммарной работе L+L' также применимо неравенство (3.8.3). Следовательно,

,

или

.

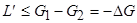Иными словами, работа, которую совершает термодинамическая система в изобарно-изотермическом процессе, не превосходит убыли её термодинамического потенциала Гиббса.

Рассмотрим некоторые свойства термодинамического потенциала Гиббса однородной системы, считая его функцией от независимых переменных (p,T). Найдем дифференциал G:

,

и воспользуемся основным термодинамическим равенством

,

в результате получим, что

,

откуда находим частные производные от потенциала Гиббса:

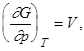
. (2.1.22)

В первое уравнение (2.1.22) входят параметры состояния p,v,T. Следовательно, оно представляет собой уравнение состояния. Это нетрудно проверить для идеального газа. Второе уравнение (2.1.22) позволяет выразить энтропию через потенциал Гиббса. Можно показать, что любая термодинамическая величина может быть выражена через потенциал Гиббса и его производные. Функции, обладающие тем свойством, что через их значения и значения их производных может быть выражена любая термодинамическая величина системы носят название характеристических функций. Потенциал Гиббса, как и свободная энергия, являются характеристическими функциями.

Дата добавления: 2015-06-27