Высказывания и операции над ними. Формулы

Введение

Дневной и сокращенной формы обучения

Обучающихся по направлению

230200 – "Информационные системы"

Данное методическое указание рассчитано на 3 практических занятия (6 часов) и является первым в серии методических указаний раздела «Математическая логика».

Цель занятий - овладение основами алгебры высказываний и булевых функций и навыками решения практических задач.

Математическая логика, как и классическая логика, исследует процессы умозаключений и позволяет из истинности одних суждений делать выводы об истинности или ложности других, независимо от их конкретного содержания. Использование в логике математических методов (алгебраизация логики и построение логических исчислений) дало начало развитию новой области математики, называемой «Математической логикой». Основная задача математической логики – формализация знаний и рассуждений. Математика является наукой, в которой все утверждения доказываются с помощью умозаключений, поэтому математическая логика, по существу, – наука о математике.

Математическая логика дала средства для построения логических теорий и вычислительный аппарат для решения задач. Математическая логика и теория алгоритмов нашли широкое применение в различных областях научных исследований и техники (например, в теории автоматов, в лингвистике, в теории релейно-контактных схем, в экономических исследованиях, в вычислительной технике, в информационных системах и др.). Основные понятия математической логики лежат в основе таких ее приложений, как базы данных, экспертные системы, системы логического программирования. Эти же понятия становятся методологической основой описания анализа и моделирования автоматизированных интегрированных производств.

В данных методических указаниях рассматриваются только темы, связанные с алгеброй высказываний. Напомним, что алгебраической структурой или алгеброй называется структура, образованная некоторым множеством вместе с введенными на нём операциями.

В алгебре логики широко используются алгебраический и функциональный языки. При алгебраическом подходе логические операции интерпретируют как алгебраические, действующие на множестве двух элементов. При функциональном подходе каждой из логических операций и формул сопоставляется определённая двузначная функция. Мы будем рассматривать оба подхода и изложение материала вести параллельно.

Высказыванием называется всякое утверждение, о котором можно вполне определенно и объективно сказать истинно оно или ложно.

Например, утверждение "2 > 0" является высказыванием и оно истинно, а утверждение "2 < 0" - ложно, утверждение "x²+y²=z²" высказыванием не является, так как оно может быть, как истинным, так и ложным при различных значениях переменных x, y, z. Высказывание полностью определяется своим истинностным значением, условимся значение истинности высказывания обозначать буквой "И" или 1, если высказывание истинно, и буквой "Л" или 0, если высказывание ложно.

Различают высказывания простые и сложные, высказывание называется простым, если никакая его часть не является высказыванием. Простые высказывания будем обозначать начальными заглавными буквами латинского алфавита A, B, C или A₁, A₂,.... Сложные высказывания характеризуются тем, что образованы из нескольких простых высказываний с помощью логических операций, т.е. являются формулами алгебры высказываний.

Обозначим B = {1, 0}. Определим операции на множестве B.

Отрицанием высказывания A называется высказывание, которое принимает значение истина, если A ложно, и наоборот. Отрицание обозначается 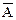(ØА) и является унарной операцией.

Пусть А и В - некоторые элементарные высказывания, введем бинарные операции над ними.

Конъюнкцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда истинны оба высказывания A и B. Обозначается конъюнкция - A 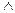B (А&В).

Дизъюнкцией высказываний A и B называется высказывание, которое принимает значение истина, если истинно хотя бы одно из высказываний A или B. Обозначается дизъюнкция - A 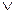B.

Импликацией высказываний A и B называется высказывание, которое принимает значение ложь тогда и только тогда, когда A истинно, а B ложно. Обозначается А®В.

Эквиваленцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда высказывания A и B имеют одинаковые значения. Обозначение операции - А~В (АºВ).

Логические операции определяются, также, с помощью таблиц, называемых таблицами истинности. Приведем сводную таблицу истинности для всех введенных логических операций.

A	B	ØA	AÙB	AÚB	A®B	A~B

Пропозициональной (высказывательной) переменной называется переменная, значениями которой являются простые высказывания. Обозначим высказывательные переменные через X₁, X₂,..., X_n.

Понятие формулы алгебры высказываний вводится по индукции. Формулами алгебры высказываний являются:

1) логические константы 1, 0;

2) пропозициональные переменные;

3) если А и В формулы, то каждое из выражений Ø А, (А Ù В), (А Ú В), (А ® В), (А ~ В) есть формула;

4) других формул, кроме построенных по пп. 1) - 3), нет.

Обозначим через M – множество всех формул алгебры высказываний, M является замкнутым относительно логических операций.

Для формулы построенной по п. 3 формулы A и B называются подформулами. Порядок выполнения операций в формуле определяется их приоритетом. Список логических операций в порядке убывания приоритета: 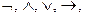~. Изменение порядка выполнения операций, как и в алгебраических операциях, производится с помощью круглых скобок.

В соответствии с таблицами истинности операций можно построить таблицу истинности формулы. Для этого необходимо:

1. Пронумеровать простые высказывания в алфавитном порядке.

2. Для каждого элементарного высказывания рассмотреть все возможные наборы значений истинности. Всего возможно 2ⁿ комбинаций, где n - число элементарных высказываний. Это количество строк в таблице.

3. Пронумеровать сложные высказывания, содержащие одну логическую операцию, затем сложные высказывания, содержащие две логических операции, и т.д., увеличивая сложность высказываний в соответствии с порядком выполнения операций.

4. Вычислить значения истинности всех сложных высказываний. Столбец с последним номером будет содержать значение истинности для всей логической формулы.

Задание. Построить таблицу истинности формулы

Ø(АÙВ) ® ØАÚС.

Решение.

1. Пронумеруем простые высказывания в алфавитном порядке А-1, В-2, С-3.

2. Каждый набор значений истинности элементарных высказываний изобразится набором ИИИ, ИИЛ, ИЛИ и т. д. Для нашего примера число комбинаций равно 8-ми, то есть таблица истинности будет содержать 8 строк.

3. Пронумеруем сложные высказывания формулы: АÙВ - 4; Ø(AÙB) - 5; ØA - 6; ØAÚС - 7; конечная операция ® - 8.

4. Вычислим последовательно значения истинности сложных высказываний.

Ø (A Ù B)	®	Ø A Ú С
Л Л И И И И И И	и и и и л л л л	И И Л Л Л Л Л Л	и и л л и и л л	И И И Л И И И И	л л л л и и и и	и и и и л л л л	и л и л и и и и	и л и л и л и л

Формулы А и В называются эквивалентными (обозначается А ~ В), если при любых значениях высказывательных переменных значение формулы А совпадает со значением формулы В.

Формула называется выполнимой, если существует такой набор значений переменных, при которых эта формула принимает значение И.

Формула называется опровержимой, если существует такой набор значений переменных, при которых эта формула принимает значение Л.

Формула называется тождественно истинной (ТИ-формулой) или тавтологией, если эта формула принимает значение И при всех наборах значений переменных.

Формула называется тождественно ложной (ТЛ-формулой) или противоречием, если эта формула принимает значение л при всех наборах значений переменных.

Так как логические формулы используются в операторах языков программирования и языков баз данных, то актуальными являются задачи определения эквивалентности, выполнимости, опровержимости, тождественной истинности и ложности формул. Такие задачи могут решаться с помощью построения таблиц истинности, однако существуют менее громоздкие способы решения этих задач, которые будут обсуждаться в параграфах 3,4.

Варианты заданий.

1. Построить таблицу истинности для формулы:

а) (Ø (P ® Ø(Q Ù P)) ® (P Ú R));

б) ((P ® (Q ® R)) ® ((P ® Q) ® (P ® R)));

в) ((P Ù (Q Ú ØP)) Ù ((ØQ ® P) Ú Q));

г) (AÙØB)Ú(ØAÙB); д) Ø((A~B) ~ (A®B)Ù(B®A));

е) (A®B)Ù(B®С)®(A®С); ж) (((P ® Q) Ú (P®(Q Ù P)));

з) (ØA Ù B) ® (ØB Ú A); и) ((A ® ØB) ® C) Ú ØA;

к) Ø(A Ù ØB) ® (B Ú C); л) C ® (Ø(A Ú C) ® A) ~ B;

м) ((P Ù (Q ® P)) ® ØP); н) (((P Ù ØQ) ® Q) ® (P ® Q));

о) (A ® B) Ú ØB; п) (A ~ B) ® (ØA Ú B).

2. Доказать выполнимость формул:

а) ((Q ® (P Ù R)) Ù Ø((P Ú R) ® Q));

б) Ø(P ® ØP); в) ((P ® Q) ® (Q ® P)).

3. Доказать тождественную истинность формул:

а) ((P ® R) ® ((Q ® R) ® ((P Ú Q) ® R)));

б) ((Q ® R) ® ((P Ú Q) ® (P Ú R)));

в) ((P ® Q) ® ((P ® (Q ® R)) ® (P ® R)));

г) ((P ® Q) ® ((Q ® R) ® (P ® R)));

д) ((P ® Q) Ú (Q ®P)); е) ((P ® Q) Ú (P ® ØQ));

ж) (P ® (Q ® (P Ù Q))); з) ((ØP ® ØQ) ® (Q ® P));

и) (P ® (Q ®P)); к) ((P Ù Q) ® P);

л) (P ® (P Ú Q)); м) ((P ® Q) ® ((P ® ØQ) ® ØP));

н) (((P ® Q) ® P) ® P); о) (ØP ® (P ® Q));

п) (A ~ B) ® (A ® B); р) ((ØQ ® ØP) ® ((ØQ ® P) ® Q)).

4. Являются ли следующие формулы тождественно ложными:

а) ((A ® B) Ù B) ®A; б) ØA ® (A Ú B);

в) Ø(A ® B) ~ (ØA ÚB); г) Ø(A ® B) ~ Ø(A Ù ØB);

д) Ø(A ® B) ® ((B ® C) ® (A ® C)).

5. При каких значениях переменных X, Y, Z, U, V, W следующие формулы выполнимы:

а) (((X ® (Y Ù Z)) ® (ØY ® ØX)) ® ØY);

б) ((X ÙY) Ú (X Ù Z) Ú (Y Ù Z) Ú (UÙ V) Ú (UÙ W) Ú (V Ù W) Ú Ú (ØX Ù ØY));

в) (((X Ú Y) Ú Z) ® ((X Ú Y) Ù (X Ú Z)));

г) (((X Ú Y) Ù (Y Ú Z) Ù (Z Ú X)) ® (X Ù Y Ù Z));

д) ((X Ú Y) ® ((ØX Ù Y) Ú (X Ù ØY))).

6. Доказать эквивалентности:

а) (A Ù (B Ù C)) ~ ((A Ù B) Ù C); б) (A Ù A) ~ A;

в) (A Ú (B Ù A)) ~ A; г) (A ® B) ~ (ØA Ú B);

д) Ø(A Ù B) ~ (ØA Ú ØB); е) Ø(A ® B) ~ (A Ù ØB);

ж) Ø(A Ú B) ~ (ØA Ù ØB); з) (A Ù B) ~ (B Ù A);

и) (A Ù (B Ú A)) ~ A; к) (A Ú A) ~ A;

л) (A Ú B) ~ (B Ú A); м) ØØA ~ A;

н) (A Ù (B Ú C)) ~ ((A Ù B) Ú (A Ù C);

о) (A Ú (B Ú C)) ~ ((A Ú B) Ú C);

п) (A Ú (B Ù C)) ~ ((A Ú B) Ù (A Ú C)).

7. Являются ли эквивалентными условия выхода в операторах цикла:

а) while (i<n)and(a[i]<>x)and(not marked[i]);

б) while not((i>=n)or(a[i]=x)or(marked[i]));

в) until not((i<n)or(a[i]<>x))or(marked[i]).

Дата добавления: 2015-06-27