
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентность и преобразование формул
|
|
|
|
Введем на множестве M отношения следования и эквивалентности.
Формула B следует из формулы A (обозначается A 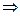 B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
Формула A эквивалентна формуле B (обозначается A ~ B), если они следуют друг из друга, то есть A 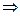 B и B
B и B 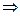 A. Легко показать, что это определение эквивалентно определению, введенному в п.1.
A. Легко показать, что это определение эквивалентно определению, введенному в п.1.
Теорема 3.1. Формула B следует из формулы A тогда и только тогда, когда тождественно истинна формула A 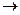 B.
B.
Теорема 3.2. Формула A эквивалентна формуле B тогда и только тогда, когда тождественно истинна формула A ~ B.
Эквивалентность формул является отношением эквивалентности, поэтому множество M можно разбить на классы эквивалентности, включив в один класс эквивалентные между собой формулы. Каждой формуле U соответствует класс эквивалентности, который обозначается [ U ].
Теорема 3.3. Если A есть некоторая подформула формулы U и A эквивалентна формуле B, то формула, полученная заменой A в формуле U на B, эквивалентна U. Иными словами, если A ~ B, то U (A) ~ U (B).
Например, так как A®B ~ 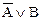 , то (A®B)ÙC ~
, то (A®B)ÙC ~ 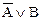 ÙC.
ÙC.
Следствие. Если U~A и V~B, то:
1) U 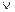 V ~ A
V ~ A 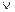 B;
B;
2) U 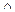 V ~ A
V ~ A 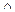 B;
B;
3) U 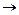 V ~ A
V ~ A 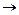 B;
B;
4) (U ~ V) ~ (A ~ B);
5) 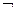 U ~
U ~ 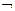 A.
A.
Теорема 3.3 и ее следствие позволяют преобразовывать формулы, упрощая их, и доказывать эквивалентность формул. Приведем список основных тавтологий, выражающих свойства логических операций.
1. Коммутативность:
X ÙY ~ Y ÙX, X ÚY ~ YÚX.
2. Ассоциативность:
(X ÙY)ÙZ ~ X Ù(YÙZ), (XÚY)ÚZ ~ XÚ(YÚZ).
3. Идемпотентность:
XÙX ~ X, XÚX ~ X.
4. Законы поглощения:
XÚX 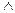 Y ~ X, X
Y ~ X, X 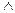 (XÚY) ~ X.
(XÚY) ~ X.
5. Взаимная дистрибутивность конъюнкции и дизъюнкции:
X Ù(YÚZ) ~ (X ÙY)Ú(X ÙZ), XÚ (YÙZ) ~ (XÚY)Ù(XÚZ).
6. Свойства констант:
XÙЛ ~ Л, XÙИ ~ X, XÚИ ~ И, XÚЛ ~ X.
7. Законы де Моргана:
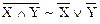 ,
, 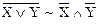 .
.
8. Закон двойного отрицания:
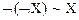 .
.
9. Закон противоречия:
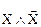 ~ Л.
~ Л.
10. Закон исключенного третьего:
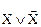 ~ И.
~ И.
Тождественная истинность всех формул (кроме законов поглощения) уже доказана непосредственно построением таблиц истинности.
Задание. Доказать 1-й из законов поглощения.
Решение.
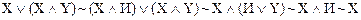 .
.
Приведем еще несколько эквивалентностей, имеющих широкое применение.
11. 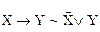 .
.
12. 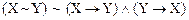 .
.
13. Склеивание:
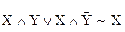 ,
, 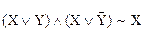 .
.
Формула называется приведенной, если она содержит операции конъюнкции, дизъюнкции и операцию отрицания, относящуюся к высказывательным переменным.
Теорема 3.4. Каждый класс эквивалентности [ U ] может быть представлен приведенной формулой, т.е. для любой формулы U 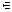 M существует приведенная формула V.
M существует приведенная формула V.
Приведенная формула для данного класса эквивалентности не является единственной. Определим порядок построения приведенной формулы.
1. Удаляются операции импликация и эквиваленция по формулам 11, 12.
2. Операции отрицания спускаются до высказывательных переменных с помощью законов де Моргана и двойного отрицания.
3. Если это возможно, то полученная приведенная формула упрощается с помощью свойств 3, 4, 5, 6, 9, 10.
Таким образом, проверить эквивалентность формул, тождественную истинность и ложность формулы или упростить ее можно с помощью этого алгоритма.
Задание. Упростить формулу 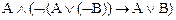 .
.
Решение. (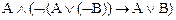 ) ~
) ~
~ (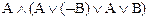 ) ~ (
) ~ (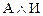 ) ~ A.
) ~ A.
Формула U* называется двойственной к приведенной формуле U, если она получена заменой операций конъюнкции на дизъюнкции и наоборот.
Теорема 3.5 (принцип двойственности). Пусть U (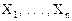 ) – приведенная формула, тогда
) – приведенная формула, тогда
U* (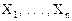 ) ~
) ~ 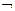 U(
U( 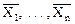 ).
).
В автоматическом управлении и при эксплуатации вычислительных машин приходится иметь дело с переключательными схемами (релейно-контактными, полупроводниковыми), состоящие из сотен реле, полупроводников, магнитных элементов. Переключательная схема состоит из переключателей (например, кнопочные устройства, электромагнитные реле, полупроводниковые элементы и т.п.) и соединяющих их проводников. При конструировании таких схем существенную помощь может оказать алгебра высказываний: можно построить схему, выполняющую требуемые функции (синтезирование схемы) или изучить действие построенной схемы и возможно ее упростить (анализ схемы).
Каждой схеме ставится в соответствие формула алгебры высказываний, и каждая формула реализуется с помощью некоторой схемы. Покажем, как установить такое соответствие. Каждому переключателю P ставится в соответствие высказывательная переменная P, которая истинна тогда и только тогда, когда переключатель P замкнут. Схеме с последовательным соединением переключателей P и Q соответствует формула, являющаяся конъюнкцией высказавательных переменных, соответствующих этим переключателям, 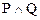 . Схеме с параллельным соединением переключателей P и Q соответствует формула, являющаяся дизъюнкцией высказавательных переменных, соответствующих этим переключателям,
. Схеме с параллельным соединением переключателей P и Q соответствует формула, являющаяся дизъюнкцией высказавательных переменных, соответствующих этим переключателям, 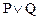 . Два переключателя P и
. Два переключателя P и 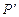 могут быть связаны так, что когда P замкнут, то
могут быть связаны так, что когда P замкнут, то 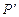 разомкнут. Тогда переключателю
разомкнут. Тогда переключателю 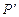 ставится в соответствие переменная
ставится в соответствие переменная 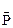 , являющаяся отрицанием P.
, являющаяся отрицанием P.
Задание. Упростить схему
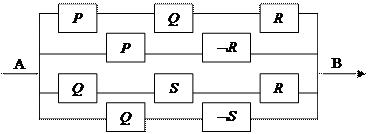
Решение. Запишем формулу, соответствующую схеме, по приведенным выше правилам
U = 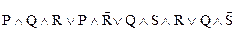 .
.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 571; Нарушение авторских прав?; Мы поможем в написании вашей работы!