Полные системы операций. Алгебра Жегалкина

Система операций å называется полной, если любая логическая операция может быть представлена формулой над å.

Так как всякая формула может быть представлена приведенной формулой, то система å₀ = {Ù, Ú, 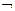} - полна. Полной будет и любая система å, через операции которой можно выразить конъюнкцию, дизъюнкцию и отрицание.

Если все операции полной системы å^* представимы формулами над системой å, то å полна, в этом случае говорят, что å сводится к å^*.

Алгебра над множеством логических функций с двумя операциями Ù и Å называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:

, ,

, ,

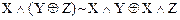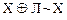а также ассоциативность, коммутативность, идемпотентность конъюнкции и свойства констант.

Задание. Доказать полноту системы å₅ = {Ù, Å}.

Решение. Сведем систему å₅ к полной системе å₀.

.

Доказательство неполноты системы операций необходимо проводить в терминах булевых функций.

Система булевых функций F называется полной, если любая функция может быть реализована формулой над F.

Замыканием множества F (обозначается [F]) называется множество всех булевых функций, реализуемых формулами над F. Класс функций называется замкнутым, если [F] = F. Примеры замкнутых классов.

1. Класс функций, сохраняющих 0.

.

2. Класс функций, сохраняющих 1.

.

3. Класс самодвойственных функций.

.

4. Класс монотонных функций.

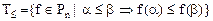, где

.

5. Класс линейных функций.

.

Теорема 5.1 (Поста). Система булевых функций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию и хотя бы одну нелинейную функцию.

Если в произвольной формуле алгебры Жегалкина, реализующей булеву функцию f, раскрыть скобки и произвести все возможные упрощения, то получится формула, имеющая вид суммы произведений, то есть полинома по mod 2. Такая формула называется полиномом Жегалкина для данной функции. Таким образом, линейной называется функция, полином Жегалкина которой линеен.

Задание. Представить формулу (x₁ Ú x₂)( Ú x₁x₃) в виде полинома Жегалкина.

Решение.

(x₁ Ú x₂)( Ú x₁x₃) = (x₁x₂Å x₁Å x₂)Ù(x₁ x₃Å x₁x₃Å ) =

= x₁ (x₂ Å 1) x₃ Å x₁ x₂ x₃ Å x₁ x₃ Å x₁ x₂ x₃ Å x₁ (x₂ Å 1) =

= x₁ x₂ x₃ Å x₁ x₂ Å x₁

Теорема 5.2. Для всякой логической функции существует полином Жегалкина, и притом единственный.

Варианты заданий.

1. Доказать полноту систем операций:

а) å₁= {Ù, ^¾}; б) å₂= { Ú, ^¾};

в) å₃ = { | }; г) å₄ = {¯ };

д) å₅ = {®, Ø}; е) å₆ = {Å, Ú}.

2. Доказать неполноту систем операций:

а) å₁ = {Ù, Ú, ®}; б) å₂ = {Ø};

в) å₃ = {Ù,Ú,®,~}.

3. Представить формулу в виде полинома Жегалкина:

а) x₁ 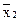Ú x₃; б) x₁ x₂ Ú .

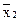Дата добавления: 2015-06-27