Теоретическая часть. Постановку задачи дискриминантного распознавания образов см

Постановку задачи дискриминантного распознавания образов см. в теоретической части первого варианта выполнения работы. Здесь будет рассмотрен только сам метод решающих функций.

Решающей функцией 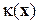для двух классов 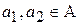называется такая функция 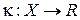, что 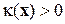, если образ 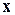принадлежит классу 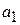, и 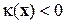, если образ 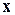принадлежит классу .

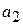Обычно рассматриваются не произвольные решающие функции, а лишь функции, относящиеся к некоторому параметрическому семейству, элементы которого 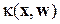определяются вектором параметров 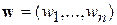, где n – количество параметров. Выбор конкретных значений параметров 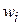соответствует выбору решающей функции. Тогда решение задачи распознавания образов сводится к определению оптимальных значений параметров по обучающей выборке.

Мы рассматриваем задачу построения решающих функций для случая двух классов 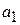и 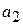. Как и раньше, в задаче распознавания имеются исходные данные: 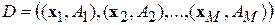– обучающая выборка из M элементов, в которой 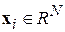– образы, представленные N -компонентными векторами признаков, а 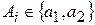– соответствующие им классы.

Важное параметрическое семейство составляют линейные решающие функции. Поиск линейных решающих функций проще как с теоретической, так и с практической точки зрения, а классификаторы, построенные на их основе, являются также и наиболее эффективными по отношению к требуемым вычислительным ресурсам. Линейные решающие функции задаются следующим образом:

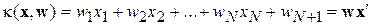, (12)

где 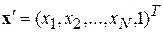– пополненный вектор признаков, а 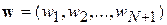– вектор весов, который требуется определить по обучающей выборке, исходя из условий: 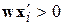, есл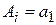и и 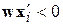, если 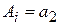. Разделяющая поверхность, задаваемая уравнением 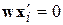, в данном случае будет гиперплоскостью.

Чтобы представить эти условия единообразно, обычно пользуются следующим приемом. Пусть 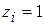, есл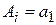и , и 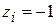, если 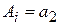, тогда ограничения на вектор параметров будут следующие:

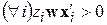. (13)

В зависимости от критерия качества и метода поиска параметров, максимизирующих этот критерий, могут быть построены различные процедуры нахождения линейных решающих функций.

Одной из идей здесь является применение классического метода наименьших квадратов (МНК). Необходимо, чтобы решающая функция правильно классифицировала образы обучающей выборки. Это можно выразить в виде следующего условия: 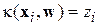. Тогда задача распознавания сводится к задаче аппроксимации, для которой в рамках МНК можно записать следующую целевую функцию:

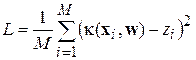. (14)

Удобство линейных решающих функций в том, что для их нахождения используется линейный МНК, имеющий эффективное решение. Для определения значений параметров, при которых достигается минимум критерия (14), продифференцируем его и получим систему линейных уравнений:

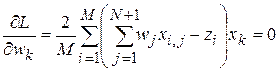, (15)

которую не представляет сложности решить.

Не любые два набора точек в 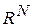разделяются гиперплоскостью, задаваемой линейной решающей функцией, а значит, не все образы в таких наборах могут быть корректно классифицированы с помощью линейной решающей функции. Это является платой за простоту и вычислительную эффективность линейных методов. Нелинейные методы сложны и вычислительно трудоемки. К счастью, существует стандартный прием, позволяющий расширять процедуры построения линейных решающих функций на нелинейные функции. Этот прием заключается в том, что вводятся обобщенные решающие функции вида

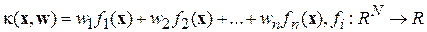. (16)

В частности, несложно получить линейные решающие функции, используя 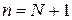и .

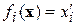Функции 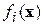предполагаются известными заранее, то есть имеется возможность однозначно получить их значения для любого вектора 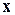. Тогда решающие функции вида (16) оказываются линейными по неизвестным параметрам 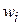, и несложно убедиться, что любой метод, предназначенный для нахождения параметров линейных решающих функций, также будет работать и для обобщенных решающих функций.

Один из стандартных способов задания обобщенных решающих функций – это представление их в виде многочленов (при этом, обычно используются ортонормированные системы функций, например, многочлены Лежандра или Эрмита). При этом, однако, количество параметров в обобщенной решающей функции перестает быть фиксированным.

На практике при полуавтоматическом распознавании образов варианты обобщенной решающей функции можно задавать вручную, подбирая наиболее подходящие дополнительные признаки .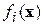

Дата добавления: 2015-06-27