Теоретическая часть. Изучение методов анализа пространства признаков

Изучение методов анализа пространства признаков

Цель работы – ознакомиться с методами анализа пространства признаков в рамках задач кластеризации и выбора признаков, а также освоить их применение в различных условиях, определяемых характером распределения образов обучающей выборки. Данная работа имеет два варианта выполнения.

Вариант 1

Задание по работе:

1. Изучить теоретическую часть работы.

2. Реализовать метод k внутригрупповых средних.

3. Путем варьирования взаимного расположения и формы кластеров, образуемых образами обучающей выборки, определить ограничения метода кластеризации.

Постановка задачи выделения кластеров в пространстве признаков

В задаче распознавания без учителя машинной системе предоставляется лишь совокупность образов 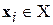, i =1,…, M. При этом на основе этих образов система должна сформировать некое множество классов 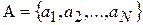и построить решающее правило .

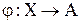Поскольку решающее правило относит каждый образ из обучающей выборки к одному из классов, то задача, по сути, сводится к тому, чтобы объединить образы обучающей выборки в группы (на основе которых и формируются классы). Такое объединение называется группированием. Здесь возникает вопрос: на каком основании какие-то образы следует относить к одной группе, а какие-то – к другой?

Один из интуитивно очевидных ответов на этот вопрос заключается в том, что объединяться должны похожие друг на друга образы. Степень сходства определяется расстоянием в пространстве признаков. Выбор метрики, однако, во многом произволен, хотя чаще всего используют евклидово расстояние. Если в классы объединяются наиболее близко расположенные друг к другу образы, то задача группирования превращается в задачу кластеризации, то есть в задачу поиска кластеров (областей, содержащих компактно расположенные группы образов).

Алгоритм k внутригрупповых средних

Алгоритм k внутригрупповых средних (или кратко алгоритм k средних) требует задания числа кластеров, исторически обозначаемых через k. Здесь для обозначения числа классов будет использоваться переменная d, а через 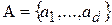будет обозначаться множество классов. Алгоритм состоит из следующих шагов:

1. Каждому из d кластеров произвольным образом назначаются их центры (или эталонные образы) 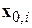. Часто в качестве этих центров выступают первые d образов обучающей выборки .

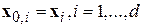2. Каждый образ выборки относится к тому классу, расстояние до центра которого минимально:

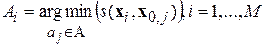, (17)

где ­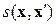– функция расстояния, в качестве которой может использоваться как евклидово расстояние, так и другие метрики, например, полезным может быть нормированное евклидово расстояние:

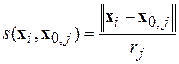, (18)

где r_j – размер j -го кластера. Этот размер вычисляется как внутриклассовое расстояние (среднеквадратичное расстояние от образов класса до его центра).

3. Центры кластеров пересчитываются, исходя из того, какие образы к каждому из них были отнесены: 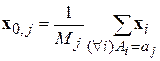, где 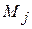– количество образов, попавших в класс 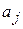. После пересчитываются радиусы кластеров: .

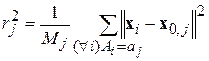4. Шаги 2 и 3 повторяются, пока не будет достигнута сходимость, то есть пока классы не перестанут изменяться.

Дата добавления: 2015-06-27