Теоретическая часть. При выборе признаков требуется найти некоторое оптимальное преобразование , где – исходное пространство признаков и – результирующее пространство

При выборе признаков требуется найти некоторое оптимальное преобразование 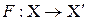, где – исходное пространство признаков и 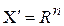– результирующее пространство признаков. В качестве исходных данных здесь выступает набор векторов 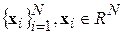без информации об их принадлежности классам. Несложно заметить, что в постановке задачи нигде в явном виде не указывается, что исходные объекты, векторы признаков которых поступают на вход системы, могут относиться к различным классам. В связи с этим обычно рассматривают критерии оптимальности преобразования 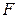, напрямую не связанные с проблемами распознавания образов.

Анализ главных компонент (АГК; principal component analysis, PCA) – это один из классических методов второго порядка, предназначенный для выбора признаков. В данной работе изучается линейный АГК. Суть этого метода в следующем.

Предположим, что мы хотим уменьшить размерность векторов признаков таким образом, чтобы по образам, описанным с помощью новых признаков, можно было бы как можно более точно восстановить исходные образы. Рассмотрим сначала случай .

Новый признак должен являться линейной комбинацией исходных признаков, то есть должен определять некоторое направление 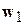в пространстве 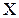. Это направление называется первой главной компонентой. Условие минимальной потери точности означает, что проекция векторов обучающей выборки на это направление должна обладать максимальной дисперсией:

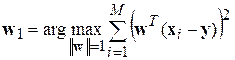, (19)

где 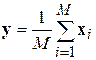– вектор средних.

Значение найденного таким образом признака для i -го вектора будет равно 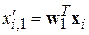. Но поскольку вектор 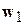соответствует некоторому направлению в исходном пространстве, то 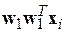– проекция i -го вектора на данное направление, а – его проекция на N -1-мерное пространство, перпендикулярное этому направлению. Это тот остаток от вектора 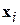, который не описывается новым признаком. В таком N -1-мерном пространстве можно найти следующее направление, проекция векторов обучающей выборки на которое обладает максимальной дисперсией. После k -1 таких итераций остатки будут иметь вид:

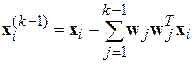, (20)

и на их основе можно будет найти очередную k -ю главную компоненту абсолютно так же, как была найдена первая и все последующие компоненты. Отметим, что направления, соответствующие главным компонентам, получаются ортогональными.

Оказывается, что поиск n главных компонент совпадает с нахождением n собственных векторов ковариационной матрицы , соответствующих n наибольшим собственным числам. Это дает возможность не искать последовательно главные компоненты, максимизируя дисперсию проекции векторов обучающей выборки, а использовать стандартные операции с матрицами для определения собственных векторов и чисел. Собственные векторы соответствуют направлению осей эллипсоида, вписанного в данные (см. рис. 2), а собственные числа – размерам осей (точнее, их квадратам).

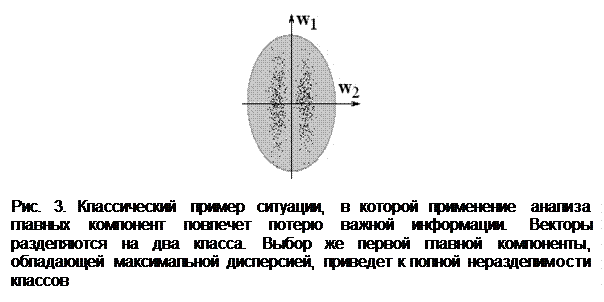
В АГК в явном виде не предполагается, что образы обучающей выборки могут относиться к объектам разных классов. В случае двух классов и больших межклассовых расстояний главная компонента может совпадать с линией, направленной от одного класса к другому, однако в общем случае это будет не так, что является очевидным ограничением, особенно в задачах распознавания образов (см. рис. 3).

Несмотря на свою ограниченность, анализ главных компонент обладает определенной привлекательностью. Этот метод опирается лишь на информацию из ковариационной матрицы и вектора средних, вычислительно прост и использует лишь классические операции с матрицами, не требуя разработки процедур поиска в пространстве параметров преобразования. В связи с этим для образов, содержащих очень большое количество признаков, АГК может стать наиболее подходящим методом предварительного выбора признаков.

Дата добавления: 2015-06-27