Исчисление высказываний. Когда мы о чем-то думаем, то непременно непроизвольно облекаем наши мысли в словесную форму

Когда мы о чем-то думаем, то непременно непроизвольно облекаем наши мысли в словесную форму.

Высказывание – это повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как, то и другое одновременно. Например, предложения «Москва – столица России», «13 – простое число» являются высказываниями. А предложения: «Который час?», а также «Город стоит на берегу реки» высказываниями не являются, поскольку первое не является повествовательным предложением, а второе – требует дополнительных сведений для определения значения высказывания.

Речевая практика привела к установлению некоторых правил, предъявляемых к высказываниям. Эти правила были сформулированы еще Аристотелем и известны, как основные законы формальной логики:

Закон тождества: каждый из предметов, о которых идет речь, все время должен оставаться самим собой.

Закон противоречия: одно и то же нельзя одновременно утверждать и отрицать.

Закон исключения третьего: любое высказывание должно быть или истинным или ложным, третьего не дано.

Таким образом, значение высказывания является верным только на момент рассмотрения высказывания. Например, значение высказывания “Идет дождь” верно только на момент рассмотрения этого высказывания. Значение высказывания зависит от предметной области. Например, высказывание “15 – простое число ” будет истинным в восьмеричной и ложным в десятичной системе счисления.

Не о всяком высказывании можно сразу сказать истинное оно или ложное. Например, утверждение, принадлежащее французскому математику Ферма: “Число 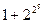- простое” будет высказыванием, поскольку это число не может быть одновременно и простым и составным. Только в 1732 году Эйлер доказал, что это высказывание ложно.

Существуют предложения, которые могут быть одновременно и ложными и истинными, это так называемые парадоксы. Например, повествовательное предложение «Я лгу» не является высказыванием. Если он лжет, то произнесенное им есть ложь и поэтому он не лжет. Если он говорит правду, то произнесенное им есть истина, и поэтому он лжет. В любом случае он лжет и не лжет одновременно.

В логике высказываний интересуются не содержанием

высказываний, а их ложностью или истинностью.

Истинное высказывание обозначается «1», а ложное «0». Множество {1,0} называется множеством истинности высказываний.

Язык исчисления высказываний, как и всякий формальный язык, задается своим алфавитом, синтаксисом и семантикой.

Алфавит языка логики высказываний состоит:

1) из пропозициональных символов (от лат. propositio – предложение), которые обозначают прописными буквами латин­ского алфавита 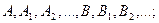Пропозициональные символы соответствуют простым или элементарным высказываниям;

2) из логических связок:

3) из запятой и скобок.

Логические связки интуитивно соответствуют частицам и союзам, которые мы используем в повседневной речи. Соответствие между ними таково:

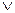, дизъюнкция – или;

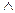, конъюнкция – и;

, отрицание – не;

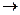, импликация – если…, то…;

, эквиваленция – …тогда и только тогда, когда…;

Синтаксис – набор правил, по которым можно сформировать составные высказывания или формулы, используя алфавит языка.

Семантика – набор правил интерпретации формул исчисления высказываний, то есть, определение: является ли эта формула истинной или ложной, если известны истинностные значения составляющих ее высказываний.

Дата добавления: 2015-06-27