Кванторные операции

Определим предикат 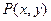- “число делится на число ”. . 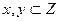Истинность этого высказывания является частичной, так как можно выбрать числа и

такие, что не делится на . А предикат - “простое число делится только на самого себя и единицу” является универсально истинным, так является истинным для любого значения x.

В логике предикатов частичная и всеобщая истинность обозначается отдельными специальными знаками – кванторами (quantum, quantity – количество; quantify – определять количество; quantifier (квантор) – соответствующее отглагольное существительное).

Если задан предикат , то особый интерес представляет рассмотрение следующих двух утверждений:

1. Неопределенное высказывание истинно для всех .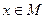

2. Неопределенное высказывание истинно хотя бы для одного элемента 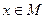, или другими словами, существует элемент множества 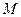, для которого - истинно.

Высказывания 1 и 2 в короткой форме будут выглядеть соответственно так:

,

.

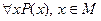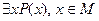Знак общности обозначается символом 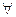– перевернутая первая буква английского слова All – все.

Знак существования обозначается символом 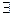– перевернутая первая буква английского алфавита Exists –существует.

Символы для кванторов в виде перевернутых английских букв были введены итальянским математиком Дж. Пеано в 90 годах XIX века.

Знак общности 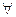заменяет в словесных формулировках слова: все, всякий, каждый, любой. Знак существования 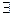употребляется вместо слов: хотя бы один, найдется, существует.

Итак, под выражением 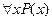понимается высказывание, истинное, когда истинно для каждого элемента из множества 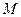и ложное в противном случае. Это высказывание уже не зависит от .

Таким образом, чтобы доказать истинность высказывания 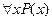нужно доказать истинность высказывания , для всех без исключения .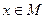

А вот, чтобы доказать ложность высказывания 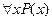достаточно указать только один элемент 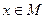, для которого утверждение является ложным. Значение 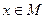, для которого ложно, называется контрпримером для выражения 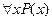. В качестве примера рассмотрим предикат , определенный на множестве натуральных чисел: - “ 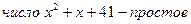”. Контпримером для выражения 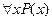является число 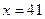, хотя для всех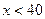 является истинным.

Под выражением 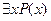понимается высказывание, которое является истинным, если существует элемент 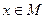, для которого истинно, и ложным в противном случае.

Таким образом, предикат можно превратить в высказывание двумя способами: подставить конкретное значение в предикат или использовать кванторы всеобщности и существования.

Переменная , входящая в предикат , называется свободной переменной. Переменная , входящая в выражение 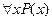, называется переменной, связанной квантором всеобщности. А переменная , входящая в выражение 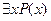- переменная, связанная квантором существования.

Кванторные операции применимы и к многоместным

предикатам. Пусть на множестве 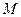задан предикат .

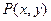Применение кванторной операции к предикату 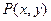по переменной ставит в соответствие двуместному предикату 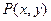одноместный предикат 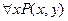, зависящий от переменной и не зависящей от переменной . К двуместному предикату можно применять кванторы, как по переменной , так и по переменной , при этом возможны следующие варианты:

; ; ; ;

; ; ; .

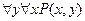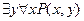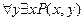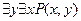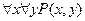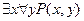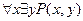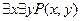Правила перестановки кванторов. Пусть 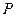- произвольная формула логики предикатов. Рассмотрим для 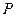произвольную, но фиксированную интерпретацию. Из определения кванторов следует, что если истинно 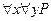, то истинно 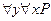и наоборот. Рассуждая аналогично, приходим к выводу, если истинно 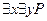, то истинно 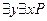. Таким образом, при перемене мест рядом стоящих одноименных кванторов получаем равносильные формулы.

Таким образом, стоящие рядом одноименные кванторы можно переставлять местами. Следовательно, формулы

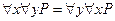и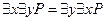

являются общезначимыми.

Разноименные кванторы можно переставлять не всегда.

Справедлива теорема: Для каждой формулы 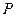и любых предметных переменных и формула

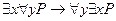
логически общезначима, а обратная импликация

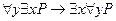
не всегда является логически общезначимой.

Для доказательства общезначимости формулы 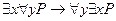зафиксируем произвольную интерпретацию

формулы 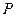и из определения кванторов получаем, что формула истинна в любой интерпретации, то есть, она общезначима.

Чтобы доказать, что формула 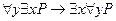не всегда является общезначимой, достаточно привести пример, где эта формула не истинна.

Пусть областью определения предиката является множество действительных чисел, а предикат = “ ”.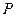

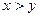Тогда высказывание 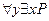означает, что для любого действительного числа существует действительное число , большее . Это высказывание является истинным.

Высказывание 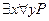означает, что существует действительное число больше любого другого числа . Это высказывание будет ложным. Тогда формула 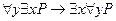не истинна в приведенной интерпретации, то есть не является логически общезначимой.

Рассмотрим предикат 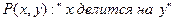, определенный на множестве целых чисел. Применение кванторных операций к предикату 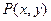приводит к восьми возможным высказываниям.

1. 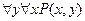- для всякого и для всякого является делителем .

2. 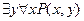- существует , которое является делителем всякого .

3. 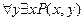- для всякого существует такое, что делится на .

4. 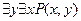- существует и существует такие, что является делителем .

5. 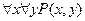- для всякого и для всякого является делителем .

6. 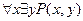- для всякого существует такое , что делится на .

7. 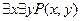- существует и существует такие, что является делителем .

8. 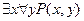- существует такое, что для всякого делится на .

Из этих восьми высказываний 2, 3, 4, 6, 7 являются истинными, а остальные ложными.

Следует обратить внимание на то, что изменение порядка следования кванторов(3) и (8) изменяет смысл высказывания и его логическое значение.

Дата добавления: 2015-06-27