
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Процедура вывода Эрбрана
|
|
|
|
Метод семантических таблиц
Для доказательства правильности умозаключения в исчислении предикатов можно пользоваться методом семантических таблиц. Как и в исчислении высказываний с помощью семантической таблицы можно доказать общезначимость формулы.
Основой для построения семантических таблиц является атомарная семантическая таблица.
На основании атомарной семантической таблицы докажем общезначимость формулы 
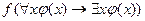
|
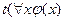
|
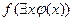
|

|
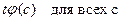
|
Формула  является общезначимой, так как соответствующая ей семантическая таблица, построенная в предположении ложности формулы, является противоречивой.
является общезначимой, так как соответствующая ей семантическая таблица, построенная в предположении ложности формулы, является противоречивой.
Таблица 4

| 
|
Продолжение табл. 4

| 
| 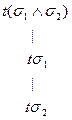
| 
|

| 
| 
| 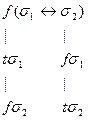
|
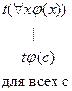
| 
| 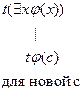
| 
|
Построим семантическую таблицу для формулы 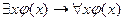 .
.
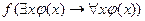
|
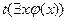
|

|
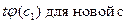
|

Данная семантическая таблица не является противоречивой, поскольку функция 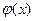 истинна при каком-то одном значении
истинна при каком-то одном значении 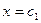 из области определения функции
из области определения функции 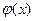 и та же функция ложна при каком-то другом значении
и та же функция ложна при каком-то другом значении  . Для всех же значений
. Для всех же значений  условие противоречивости не выполняется.
условие противоречивости не выполняется.
Далее приведены семантические таблицы для двух общезначимых формул.
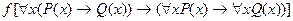
|

|

|
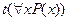
|

|
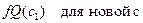
|
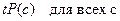
|
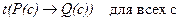


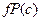
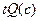
| |
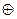
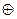

| |
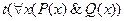

| |


| |

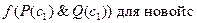
| ½

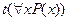
| |
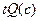


 ½
½


 ½
½  ½ ½
½ ½ 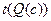




Å Å 
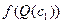
Å Å 
Раннее было установлено, что множество дизъюнктов  невыполнимо тогда и только тогда, когда оно принимает значение ложь при всех интерпретациях на любых областях. Однако в силу невозможности рассмотрения всех интерпретаций на любых областях хорошо бы найти такую специальную область интерпретации, установив на которой факт невыполнимости множества дизъюнктов, можно было бы сделать вывод о невыполнимости этого множества на любых других областях интерпретаций.
невыполнимо тогда и только тогда, когда оно принимает значение ложь при всех интерпретациях на любых областях. Однако в силу невозможности рассмотрения всех интерпретаций на любых областях хорошо бы найти такую специальную область интерпретации, установив на которой факт невыполнимости множества дизъюнктов, можно было бы сделать вывод о невыполнимости этого множества на любых других областях интерпретаций.
Такая специальная область интерпретации существует и называется универсумом Эрбрана. Универсум Эрбрана определяется так:
Шаг 1. Пусть  - множество дизъюнктов, соответствующее предложению
- множество дизъюнктов, соответствующее предложению 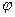 .
.
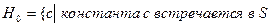

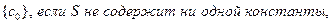
где  - новая константа (слово “новая означает, что она не встречается в
- новая константа (слово “новая означает, что она не встречается в  ). Эта новая константа выбирается произвольным образом.
). Эта новая константа выбирается произвольным образом.
Шаг  .
.
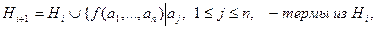
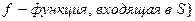
И, наконец, полагаем  .
.
Множество  всех термов, построенных из констант
всех термов, построенных из констант  и функциональных символов, встречающихся в
и функциональных символов, встречающихся в  , называется эрбрановским универсумом для
, называется эрбрановским универсумом для  , а
, а 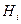 – его уровнем
– его уровнем  . Множества
. Множества 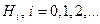 называются эрбрановскими множествами
называются эрбрановскими множествами 
Проиллюстрируем получение универсума Эрбрана на следующих примерах.
Пример 1. Пусть 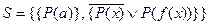
Тогда
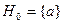 ;
;
 ;
;
 ;
;
…………………………………….
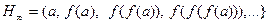 .
.
Пример 2.
Пусть 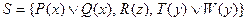
Так как не существует никаких констант в  , полагаем
, полагаем 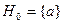 . Не существует никаких функциональных символов в
. Не существует никаких функциональных символов в  , следовательно,
, следовательно, 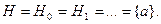
Пример 3.
Пусть 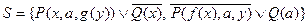 .
.
Тогда
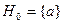 ;
;
 ;
;
 ;
;
 ………………………………………………………
………………………………………………………
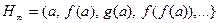 .
.
Пример 4.
Пусть 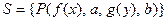 ;
;
 ;
;
 ;
;

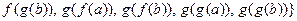 .
.
………………………………………………………
Если под выражением понимать терм, множество термов, атом, множество атомов, литеру, множество литер, дизъюнкт или множество дизъюнктов, то под фундаментальным выражением будем понимать выражение, в котором все переменные заменены элементами универсума Эрбрана. Так, фундаментальным примером дизъюнкта будем называть дизъюнкт, полученный заменой всех переменных в этом дизъюнкте элементами универсума Эрбрана таким образом, что все вхождения одной и той же переменной в дизъюнкт заменяются одним и тем же элементом универсума.
Множество фундаментальных атомов вида 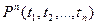 , где
, где  – все
– все 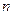 - местные предикатные символы, встречающиеся во множестве дизъюнктов
- местные предикатные символы, встречающиеся во множестве дизъюнктов  и
и 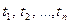 – элементы универсума Эрбрана, называется атомарным множеством или эрбрановской базой для
– элементы универсума Эрбрана, называется атомарным множеством или эрбрановской базой для  . Обозначим эрбрановскую базу через
. Обозначим эрбрановскую базу через  .
.
Пример 5.
Пусть 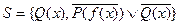 .
.
Тогда 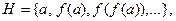

Фундаментальные примеры: 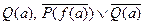 и т.п.
и т.п.
Определим теперь интерпретацию на универсуме Эрбрана и назовем ее  - интерпретацией. Говорят, что интерпретация
- интерпретацией. Говорят, что интерпретация  является
является  - интерпретацией для множества дизъюнктов
- интерпретацией для множества дизъюнктов  , если выполнены следующие соответствия:
, если выполнены следующие соответствия:
- каждому предикатному символу 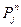 соответствует некоторое
соответствует некоторое 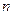 - местное отношение в
- местное отношение в  ;
;
- каждому функциональному символу  соответствует некоторая
соответствует некоторая 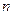 - местная функция в
- местная функция в  (т.е. функция, отображающая
(т.е. функция, отображающая 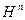 в
в  );
);
- каждой предметной константе 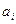 из
из  соответствует некоторая константа из
соответствует некоторая константа из  (т.е. все константы отображаются на самих себя).
(т.е. все константы отображаются на самих себя).
Пусть  является эрбрановской базой для
является эрбрановской базой для  . Тогда
. Тогда  - интерпретация
- интерпретация 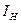 может быть представлена множеством
может быть представлена множеством  , в котором
, в котором  есть
есть  или
или  для
для 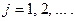 При этом, если
При этом, если  есть
есть  то
то  имеет значение “истина”, в противном случае “ложь”.
имеет значение “истина”, в противном случае “ложь”.
Пример 6. Пусть  .
.
Тогда 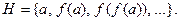
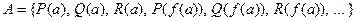 .
.
Примеры  - интерпретаций:
- интерпретаций:
 ;
;
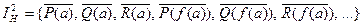 ;
;
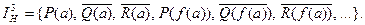
При  оба дизъюнкта выполнимы, при
оба дизъюнкта выполнимы, при  первый дизъюнкт выполним, второй нет, при
первый дизъюнкт выполним, второй нет, при  оба дизъюнкта невыполнимы, т.е. принимают значение “ложь”.
оба дизъюнкта невыполнимы, т.е. принимают значение “ложь”.
В случае если интерпретация задана не на универсуме Эрбрана, а на произвольной области  , то можно установить следующее соответствие между этими интерпретациями. Пусть дана интерпретация
, то можно установить следующее соответствие между этими интерпретациями. Пусть дана интерпретация  на некоторой области
на некоторой области  . Говорят, что
. Говорят, что  - интерпретация
- интерпретация 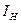 соответствует интерпретации
соответствует интерпретации  , если имеет место следующее: пусть
, если имеет место следующее: пусть 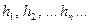 – элементы
– элементы  и пусть каждый
и пусть каждый 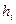 отображается на некоторый элемент
отображается на некоторый элемент  области
области  , тогда, если любой
, тогда, если любой 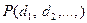 принимает значение “истина” (“ложь”) при интерпретации
принимает значение “истина” (“ложь”) при интерпретации  , то
, то 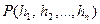 также принимает значение “истина” (“ложь”) при
также принимает значение “истина” (“ложь”) при 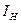 . Имеет место следующая теорема.
. Имеет место следующая теорема.
Теорема Множество дизъюнктов  невыполнимо тогда и только тогда, когда
невыполнимо тогда и только тогда, когда  ложно при всех
ложно при всех  - интерпретациях.
- интерпретациях.
Доказательство «тогда» очевидно, а «только тогда» легко доказывается от противного введением соответствия между  - интерпретацией и некоторой произвольной
- интерпретацией и некоторой произвольной
интерпретацией. В дальнейшем будем рассматривать только
 - интерпретации, и называть их просто интерпретациями
- интерпретации, и называть их просто интерпретациями  .
.
Таким образом, для установления невыполнимости множества дизъюнктов необходимо и достаточно рассмотреть только  - интерпретации.
- интерпретации.
Процедура вывода Эрбрана основывается на его теореме.
Теорема Эрбрана. Множество дизъюнктов  невыполнимо тогда и только тогда, когда существует конечное невыполнимое множество
невыполнимо тогда и только тогда, когда существует конечное невыполнимое множество 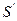 фундаментальных примеров дизъюнктов
фундаментальных примеров дизъюнктов  .
.
Таким образом, для установления невыполнимости множества дизъюнктов необходимо образовать множества  фундаментальных примеров дизъюнктов и последовательно проверять их на ложность. Теорема Эрбрана гарантирует, что, если множество дизъюнктов
фундаментальных примеров дизъюнктов и последовательно проверять их на ложность. Теорема Эрбрана гарантирует, что, если множество дизъюнктов  невыполнимо, то данная процедура обнаружит такое
невыполнимо, то данная процедура обнаружит такое 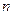 , что
, что  является ложным.
является ложным.
Процедура вывода Эрбрана состоит из двух этапов: сначала находится множество всех фундаментальных примеров дизъюнктов и затем, используя мультипликативный метод, из КНФ получают ДНФ.
Пример.
Пусть 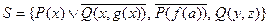 .
.
Находим 
и фундаментальные примеры дизъюнктов:
 .
.
Затем с помощью мультипликативного метода убеждаемся в невыполнимости  .
.
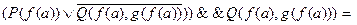

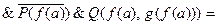 £ Ú £ = £.
£ Ú £ = £.
Недостаток процедуры вывода Эрбрана состоит в экспоненциальном росте множества фундаментальных примеров  при увеличении
при увеличении  . C помощью процедуры вывода Эрбрана удается доказать только простые теоремы.
. C помощью процедуры вывода Эрбрана удается доказать только простые теоремы.
Иной поход предложил Дж. Робинсон, который ввел принцип резолюции, являющийся теоретической базой для построения большинства методов автоматического доказательства теорем.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 2742; Нарушение авторских прав?; Мы поможем в написании вашей работы!