Вычислимые функции, частично-рекурсивные и общерекурсивные функции. Тезис Черча

ЗАНЯТИЕ 7. ТЕОРИЯ АЛГОРИТМОВ

Алгоритм – общий, единообразный, точно определенный способ решения любой задачи из данной массовой проблемы, то есть, из некоторого класса однотипных задач. Это определение алгоритма является нестрогим, так как не совсем ясно, что означает слово "способ". Это нестрогое определение алгоритма называют интуитивным. Интуитивное определение алгоритма достаточно, когда речь идет об уже найденном алгоритме решения задачи. Для доказательства существования алгоритма достаточно описать физический процесс, приводящий к решению. В этом случае можно обойтись интуитивным определением алгоритма.

Для доказательства отсутствия алгоритма требуется строгое определение алгоритма. Поиск строгого определения алгоритма ведется в трех направлениях.

Первое направление связано с уточнением понятия эффективно вычислимой функции. Значительный вклад в решение этой проблемы внесли американский математик и логик А. Черч, австрийский логик и математик К. Гедель и американский логик и математик С. Клини. Ими был выделен класс частично рекурсивных функций, имеющих строгое математическое определение. А поскольку для частично рекурсивной функции существует алгоритм ее вычисления, то был выдвинут тезис, что всякая интуитивно вычислимая функция есть частично рекурсивная функция (тезис Черча).

Второе направление связано с машинной математикой (сущность понятия алгоритма раскрывается здесь путем рассмотрения процессов, осуществляемых в так называемой машине Тьюринга). Введение понятия машины Тьюринга явилось первой и удачной попыткой дать математический эквивалент для общего интуитивного представления об алгоритме. Работы в этом направлении велись английским

математиком А. Тьюрингом задолго до появления первой электронно-вычислительной машины.

Третье направление связано с понятием нормальных алгоритмов, разработанных российским математиком А.А. Марковым.

Пусть необходимо найти алгоритм для решения задачи, в условии которой входят значения некоторой системы целочисленных параметров: 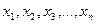, а искомым результатом является целое число .

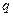Функция 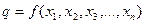- называется эффективно вычислимой, если существует алгоритм, позволяющий вычислить ее значение (здесь используется интуитивное определение алгоритма). Совокупность вычислимых функций называется совокупностью рекурсивных функций.

Элементарные вычислимые функции

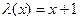(оператор сдвига или функция следования)

2. 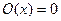(оператор аннулирования или нуль функция)

3. 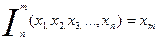, (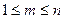) (оператор проектирования).

Эти три простейшие функции всюду определены и вычислимы.

Операции над функциями.

1. Суперпозиция функций:

Рассмотрим функции

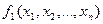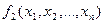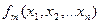, ,…, , функцию 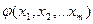и функцию 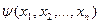, определяемую равенством =

=

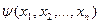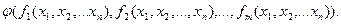
Принято считать, что функция 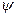получена из функции 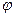, и функций 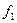, ,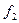…, 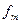суперпозицией.

Если функции 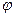, , 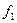,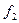…, 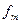всюду определены и интуитивно вычислимы, то функция 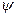также будет определена и интуитивно вычислима.

В том случае, если не все функции 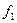, ,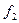…, 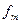зависят не от всех 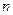аргументов, для получения суперпозиции используются фиктивные аргументы и функции проектирования.

Например, функция 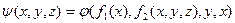получена суперпозицией из функци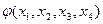й , и ; ;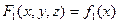

= ; .

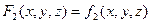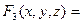
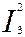
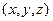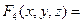
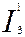
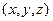2. Схема примитивной рекурсии.

Рекурсия - это способ задания функции путем определения каждого из ее значений в терминах ранее определенных значений.

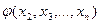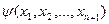Пусть имеем две функции: и , где .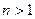

Рассмотрим новую функцию, которая удовлетворяет следующим двум равенствам

,

.

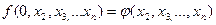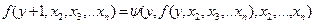Функция 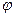зависит от 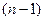аргументов, функция зависит от 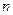аргументов, а функция 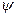зависит от 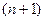аргумента.

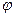Говорят, что функция получена из функций и 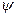по схеме примитивной рекурсии. Если функци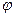и и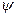

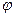интуитивно вычислимы, то будет интуитивно вычислима и функция . Если и 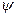всюду определены, то будет всюду определена и функция

Пусть функция 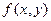задана равенствами

,

.

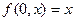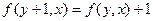Нетрудно показать, что 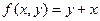. Действительно, 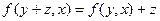. Полагая в этом равенстве 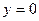, получим 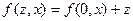или .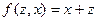

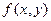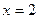Вычислить при и .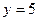

В этой задаче 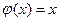, а .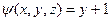

,

,

,

,

,

.

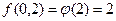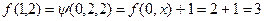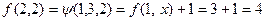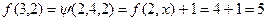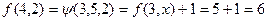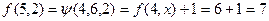Пример 1. Используя простейшие функции и оператор примитивной рекурсии, получить функцию, называемую усеченной разностью

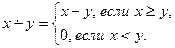
Рассмотрим функцию 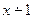, полученную из функции 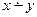фиксированием второго аргумента. Функция 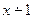удовлетворяет следующим соотношениям:

;

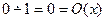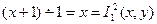, то есть она получена из простейших функци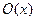й и 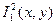с помощью оператора примитивной рекурсии.

Из определения усеченной разности следует, что функция удовлетворяет также следующим равенствам

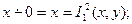
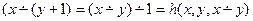
для любых 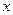и 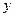. Таким образом, функция 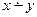получена с помощью оператора примитивной рекурсии из простейшей функции 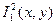и функции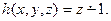

Пример 2. Показать, что функция 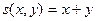может быть получена из простейших функций с помощью оператора примитивной рекурсии.

Для функции справедливы следующие тождества

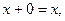
, которые можно записать в виде

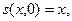
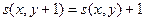или ,

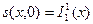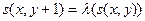, где 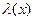- функция следования.

Таким образом, функция 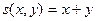получена по схеме примитивной рекурсии с использованием простейших функций: функции проектирования 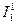и функции следования .

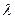Пример 3. Используя простейшие функции и оператор примитивной рекурсии, получить функцию .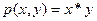

Используем очевидные соотношения для операции умножения

, .

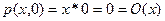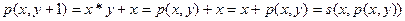Таким образом, функция 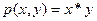получена из простейшей функции 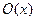, функции 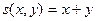, определенной в предыдущем примере, и оператора примитивной рекурсии.

3. Оператор минимизации (m - оператор)

Пусть задана некоторая функция 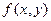. Зафиксируем 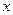и выясним, при каком у функция 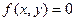. Если значений 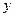, при которых 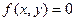, будет несколько, то отыщем минимальное значение 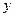, при котором 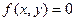. Поскольку минимальное значение 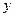будет зависеть от х, то функция 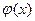определяется следующим образом: 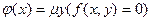. Аналогично определяется функция 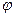нескольких переменных.

.

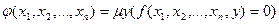Переход от функции 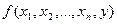к функции 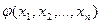называют применением - оператора. Алгоритм вычисления функции 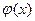включает в себя следующие шаги:

1. Вычислим 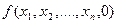. Если это значение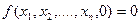 , то полагаем 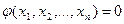. Если 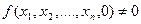, то переходим к следующему шагу.

2. Вычислим 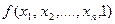. Если 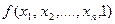= 0, то полагаем 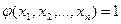. В противном случае переходим к следующему шагу.

Если для всех 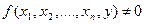, то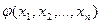

считается неопределенной.

Рассмотрим функцию 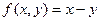, которая может быть получена с помощью оператора минимизации

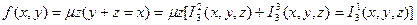
Для вычисления 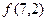положим 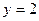, а переменной 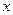будем последовательно придавать значения:

,

,

,

,

,

.

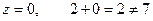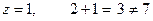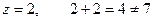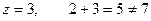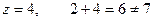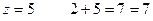Таким образом .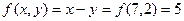

Попытаемся вычислить .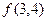

,

,

,

………………………..

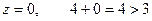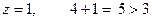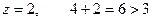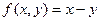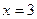Поскольку этот процесс будет продолжаться бесконечно, следовательно, функция при и 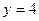не определена.

Определение 1. Функция 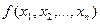называется частично рекурсивной, если она может быть получена за конечное число шагов из простейших функций при помощи операции суперпозиции, схем примитивной рекурсии и 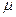- оператора.

Определение 2. Функция 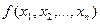- называется общерекурсивной, если она частично рекурсивна и всюду определена.

Тезис А.Черча. Каждая интуитивно вычислимая функция является частично рекурсивной.

Этот тезис нельзя доказать, так как он связывает нестрогое понятие интуитивно вычислимой функции со строгим математическим понятием частично-рекурсивной функции. Однако этот тезис можно опровергнуть, если построить пример функции интуитивно вычислимой, но не являющейся частично рекурсивной.

Дата добавления: 2015-06-27