
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод резолюций в исчислении предикатов
|
|
|
|
Метод резолюций для исчисления предикатов представляет собой комбинацию алгоритма унификации для исчисления предикатов и метода резолюций для исчисления высказываний.
Поскольку переменные во всех дизъюнктах считаются связанными кванторами всеобщности, то эти переменные можно переименовывать, чтобы избежать конфликтов во время процедуры унификации. Такое переименование переменных называется нормализацией переменных.
Рассмотрим применение метода резолюции на примерах.
Пример 1. Существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один из преподавателей не является невеждой.
Введем следующие обозначения
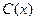 - “
- “  - студент”;
- студент”;
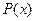 - “
- “  - преподаватель”;
- преподаватель”;
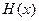 - “
- “  - невежда”;
- невежда”;
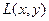 - “
- “  любит
любит  ”.
”.
На языке логики предикатов эти утверждения будут иметь вид:
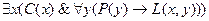 ;
;
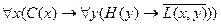 ;
;
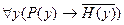 ,
,
где 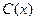 - “
- “  - есть студент”;
- есть студент”;
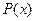 - “
- “  - есть преподаватель”;
- есть преподаватель”;
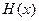 - “
- “  - есть невежда”;
- есть невежда”;
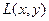 - “
- “  любит
любит  ”.
”.
Получаем ССФ последовательно для всех посылок и заключения.
Для первой посылки ССФ имеет вид: 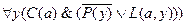 .
.
Для второй посылки ССФ имеет вид: 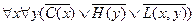 .
.
Отрицание заключения имеет такую ССФ:
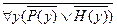 =
= 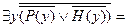
= 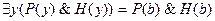 .
.
К полученному набору дизъюнктов применим метод резолюции.
1. 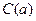 ;
;
2. 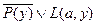 ;
;
3. 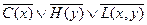 ;
;
4. 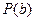 ;
;
5. 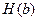 ;
;
6. 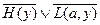 (1,3) {
(1,3) { 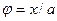 };
};
7. 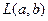 (2,4) {
(2,4) { 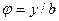 };
};
8. 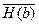 (6,7) {
(6,7) { 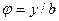 };
};
9. ð (5,8).
Пример 2.
Допустим, что посылки и заключения уже представлены в виде множества дизъюнктов
1. 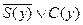 ;
;
2. 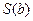 ;
;
3. 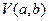 ;
;
4. 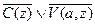 ;
;
5. 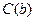 (1,2) {
(1,2) { 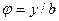 };
};
6. 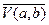 (4,5) {
(4,5) { 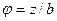 };
};
7. (3,6).
Пример 3. Преподаватели принимали зачеты у всех студентов, не являющихся отличниками. Некоторые аспиранты и студенты сдавали зачеты только аспирантам. Ни один из аспирантов не был отличником. Следовательно, некоторые преподаватели были аспирантами.
Пусть
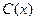 -
-  - студент,
- студент,
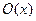 -
-  - отличник,
- отличник,
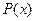 -
-  - преподаватель,
- преподаватель,
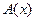 -
-  -аспирант,
-аспирант,
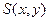 -
-  сдает зачеты
сдает зачеты  .
.
Тогда на языке исчисления предикатов имеем
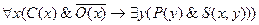 ;
;
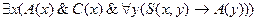 ;
;
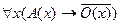 ;
;
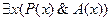 .
.
Получаем ССФ последовательно для всех посылок и заключения.
Для первой посылки ССФ имеет вид:
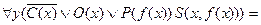

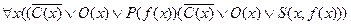 ;
;
Для второй посылки ССФ имеет вид:
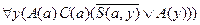 ;
;
Для третьей посылки ССФ имеет вид:
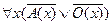 ;
;
Отрицание заключения имеет такую ССФ
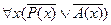 .
.
К полученному множеству дизъюнктов применим метод резолюции.
1. 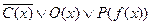 ;
;
2. 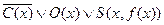 ;
;
3. 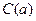 ;
;
4.  ;
;
5. 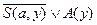 ;
;
6. 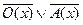 ;
;
7. 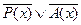 ;
;
8. 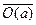 (4,6) {
(4,6) { 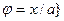 ;
;
9. 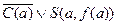 (8,2) {
(8,2) { 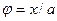 };
};
10. 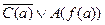 (9,5) {
(9,5) { 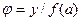 };
};
11. 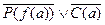 (10,7) {
(10,7) { 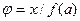 };
};
12. 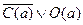 (11,1) {
(11,1) { 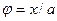 };
};
13. 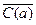 (12,8);
(12,8);
14. (3,13).
Получение пустого дизъюнкта свидетельствует о том, что сделанное предположение о ложности вывода является неверным, следовательно, заданное множество общезначимо.
Сделать такой вывод позволяют следующие теоремы о корректности и полноте метода резолюций
Теорема 1. (Корректность исчисления резолюций).
Пусть  множество дизъюнктов, и
множество дизъюнктов, и 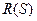 – множество резольвент
– множество резольвент  . Если множество
. Если множество 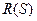 содержит пустой дизъюнкт, то
содержит пустой дизъюнкт, то  невыполнимо.
невыполнимо.
Теорема 2. (полнота исчисления резолюций).
Пусть  - множество дизъюнктов, и
- множество дизъюнктов, и 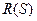 - множество резольвент
- множество резольвент  . Если множество
. Если множество  , невыполнимо, то множество
, невыполнимо, то множество 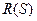 содержит пустой дизъюнкт.
содержит пустой дизъюнкт.
Контрольные вопросы и упражнения
Задание 1
Проверить правильность следующих умозаключений тремя способами: методом семантических таблиц, используя процедуру вывода Эрбрана, и методом резолюций.
1. Ни один человек не является четвероногим. Все дети – люди. Следовательно, ни один ребенок не является четвероногим.
2. Каждый, купивший билет, получает премию. Следовательно, если нет премии, то никто не покупал билетов; (В(х,у) - “x покупает y”; T(x) - “x есть билет”; P(x) - “х есть премия”; R(x,y) - “x получает у”).
3. Каждый член комитета богат и республиканец. Некоторые члены комитета – старики. Следовательно, существуют старики- республиканцы.
4. Некоторые республиканцы любят всех демократов. Ни один республиканец не любит ни одного социалиста. Следовательно, ни один демократ не является социалистом.
5. Всякое рациональное число есть действительное число. Существует рациональное число. Следовательно, существует действительное число.
6. Все рациональные числа являются действительными числами. Некоторые рациональные числа – целые числа. Следовательно, некоторые действительные числа – целые числа.
7. Все первокурсники встречаются со всеми второкурсниками. Ни один первокурсник не встречается ни с одним студентом предпоследнего курса. Существуют второкурсники. Следовательно, ни один второкурсник не является студентом предпоследнего курса.
8. Некоторые первокурсники любят всех второкурсников. Ни один первокурсник не любит никого из
студентов предпоследнего курса. Следовательно, ни один второкурсник не является студентом предпоследнего курса.
9. Борис – мальчик, у которого нет автомобиля. Анна любит только мальчиков, имеющих автомобили. Следовательно, Анна не любит Бориса.
10. Некоторым нравится Елена. Некоторые не любят никого, кому нравится Елена. Следовательно, некоторых любят не все.
11. Марк был римлянином. Цезарь был диктатором. Те римляне, которые ненавидели диктатора, пытались убить его. Римляне либо были преданы диктатору, либо ненавидели его. Марк не был предан Цезарю. Следовательно, Марк пытался убить Цезаря.
12. Никакой торговец игрушками сам себе их не покупает. Некоторые люди, покупающие игрушки, глупы. Следовательно, некоторые глупые люди не торгуют игрушками.
13. Иван и Петр – братья. Братья имеют одну фамилию. Петр имеет фамилию Сидоров. Следовательно, Иван тоже имеет фамилию Сидоров.
14. Всякое нечетное натуральное число является разностью двух квадратов. 5 является нечетным натуральным числом. Следовательно, 5 является разностью двух квадратов.
15. Когда я устал и голоден, я хочу вернуться домой. Сейчас я устал и голоден. Значит, я хочу вернуться домой.
16. Когда я устал, я хочу вернуться домой. Когда я голоден, я хочу вернуться домой или отправиться в ресторан. Сейчас я устал и голоден. Поэтому сейчас я хочу вернуться домой.
17. Перья есть только у птиц. Ни одно млекопитающее не является птицей. Значит, млекопитающие лишены перьев.
18. Имеется прилежные студенты. Ни один студент не
лишен способностей. Значит, некоторые студенты, лишенные способностей, не прилежны.
19. Все политики – лицедеи. Некоторые лицедеи – лицемеры. Значит, некоторые политики - лицемеры.
20. Ничто плодотворное не легко. Некоторые легкие вещи общедоступны. Значит, некоторые общедоступные вещи не плодотворны.
21. У неё только преданные друзья. Некоторые из ее друзей – лицемеры. Ни один лицемер не может быть преданным. Значит, все ее друзья – проходимцы.
22. Глупец был бы способен на это. Я на это не способен. Значит, я не глупец.
23. Если бы кто-нибудь мог решить эту задачу, то и какой-нибудь математик мог бы ее решить. Иванов – математик. А не может ее решить. Значит, задача неразрешима.
24. Всякий кто может решить эту задачу, - математик. Иванов не может ее решить. Значит, Иванов – не математик.
25. Всякий математик может решить эту задачу, если кто-нибудь ее может решить. Иванов – математик, а не может ее решить. Значит, задача неразрешима.
26. Всякий, кто может решить эту задачу, - математик. Ни один математик не может решить этой задачи. Значит, она не решаема.
27. Если какое-нибудь из чисел, лежащиx (строго) между 1 и 101, делит 101, то простое число, меньше 11, делит 101. Ни одно простое число, меньше 11 не делит 101. Значит, ни одно число между 1 и 101 не делит 101.
28. Никто не поймет этого сообщения, если кто-нибудь не разгадает кода. Значит, имеется кто-то, кто может понять это сообщение только, если разгадает код.
29. Любой радикал является сторонником общественного прогресса. Иные консерваторы
недолюбливают всех сторонников общественного прогресса. Значит, иные консерваторы недолюбливают все радикалов.
30. Некоторые пациенты любят докторов. Ни один пациент не любит знахарей. Значит, ни один доктор не является знахарем.
31. Тот, кто распускает этот слух, должен быть и ловким и беспринципным. Иванов не ловок, Сидоров не беспринципен. Значит, ни Иванов, ни Сидоров не распускают этот слух.
32. Ни один первокурсник не любит второкурсников. Все, живущие на первом этаже, - второкурсники. Следовательно, ни один первокурсник не любит никого из живущих на первом этаже.
Задание 2
Доказать с помощью метода резолюций.
1. 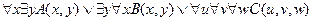 ,
,
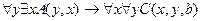 ,
,
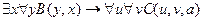 ╞
╞
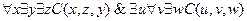 .
.
2. 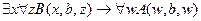 ,
,
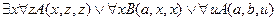 ╞
╞
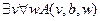 ,
,
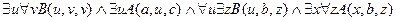 .
.
3. 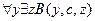 ,
,
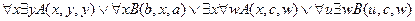 ╞
╞
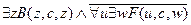 ,
,
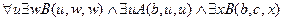 .
.
4. 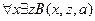 ,
,
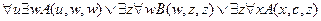 ╞
╞
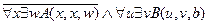 ,
,
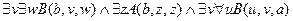 .
.
5. 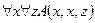 ,
,
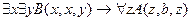 ╞
╞
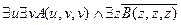 ,
,
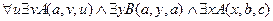 .
.
6. 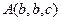 ,
,
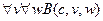 ,
,
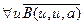 ╞
╞
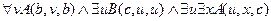 ,
,
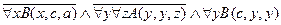 .
.
7. 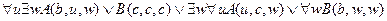 ,
,
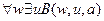 ╞
╞
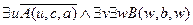 ,
,
 .
.
8. 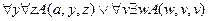 ,
,
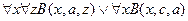 ╞
╞
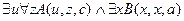 ,
,
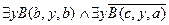 .
.
9. 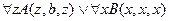 ,
,
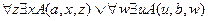 ╞
╞
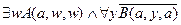 ,
,
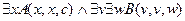 .
.
10. 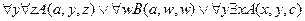 ,
,
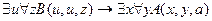 ╞
╞
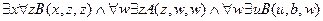 ,
,
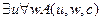 .
.
11. 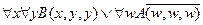 ,
,
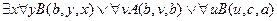 ╞
╞
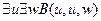 ,
,
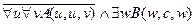 .
.
12. 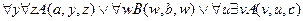 ,
,
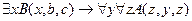 ╞
╞
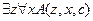 ,
,
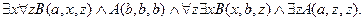
13. 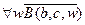 ,
,
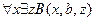 ,
,
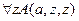 ╞
╞
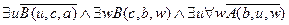 ,
,
 .
.
14. 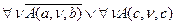 ,
,
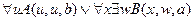 ╞
╞
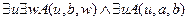 ,
,
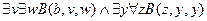 .
.
15. 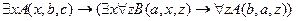 ,
,
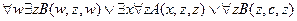 ╞
╞
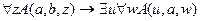 ,
,
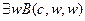 .
.
16. 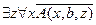 ,
,
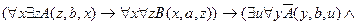
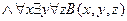 ╞
╞
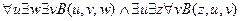 .
.
17. 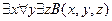 ,
,
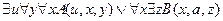 ,
,
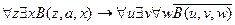 ╞
╞
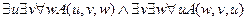 .
.
18. 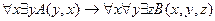 ,
,
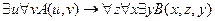 ,
,
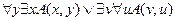 ╞
╞
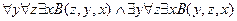 .
.
19. 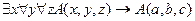 ,
,
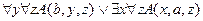 ,
,
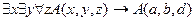 ╞
╞
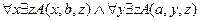 .
.
20. 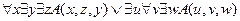 ╞
╞
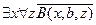 ,
,
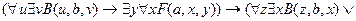
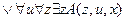 .
. 
21. 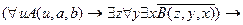
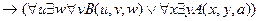 ,
,
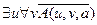 ╞
╞
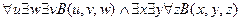 .
.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 11489; Нарушение авторских прав?; Мы поможем в написании вашей работы!