Нормальные алгоритмы Маркова

Тезис Тьюринга

(основная гипотеза теории алгоритмов)

Каждую задачу из бесконечного множества задач можно закодировать некоторым словом некоторого алфавита, а решение задачи - каким-то другим словом того же алфавита. В результате получим функцию, заданную на некотором подмножестве множества всех слов того же алфавита. Решить какую-либо задачу – значит найти значение этой функции на слове, кодирующем данную задачу. Иметь алгоритм решения всех задач данного класса – значит, иметь единый способ, позволяющий за конечное число шагов вычислять значения построенной функции для любых значений аргумента из ее области определения. Таким образом, алгоритмическая проблема – это проблема о вычислении значений функции, заданной в некотором алфавите.

Каждая функция, для вычисления которой существует

какой-нибудь алгоритм, оказывалась вычислимой посредством некоторой машины Тьюринга. Это дало повод Тьюрингу высказать гипотезу, называемую основной гипотезой теории алгоритмов, или тезисом Тьюринга:

Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция является вычислимой по Тьюрингу, то есть, когда она может вычисляться на подходящей машине Тьюринга.

Данный тезис является аксиомой. Этот тезис не может доказан методами математики, потому что он не имеет внутриматематического характера (одна сторона в тезисе – понятие алгоритма – не является точным математическим понятием). Однако этот тезис может быть опровергнут, если будет найдена функция, которая вычислима с помощью какого-нибудь алгоритма, но не вычислима на машине Тьюринга.

Теория нормальных алгоритмов была разработана русским математиком А.А. Марковым в конце 1940-х – начале 1950-х гг. ХХ в. Эти алгоритмы представляют некоторые правила по переработке слов в каком-либо алфавите, так что исходные данные и результаты являются словами в некотором алфавите.

Марковские подстановки. Алфавитом называется любое непустое множество символов. Элементы этого множества называются буквами, а последовательности букв – словами в данном алфавите. Допускается наличие пустых слов, то есть слов, не содержащих ни одной буквы. Пустое слово обозначается символом 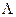. Есл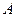и и 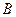два алфавита, причем, 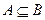то алфавит 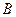называется расширением алфавита .

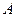Слова обозначаются латинскими буквами: 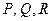(или этими же буквами с индексами). Одно слово может быть составной частью другого слова. Тогда первое слово называется подсловом второго слова или вхождением во второе. Например, если 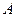- русский алфавит, то можно рассмотреть такие слова: 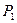= параграф, 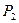= граф, 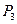=ра. Слово 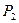является подсловом слов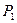а , а 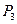- подсловом 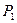и 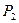, причем в 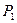оно входит дважды. Особый интерес представляет первое вхождение.

Марковской подстановкой называется операция над словами, задаваемая с помощью упорядоченной пары слов (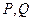), состоящая в следующем. В заданном слове 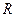находят первое вхождение слова 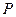, (если таковое имеется) и, не изменяя остальных частей слова 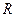, заменяют в нем это вхождение словом 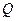. Полученное слово называется результатом применения марковской подстановки к

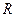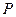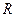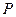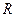слову . Если же первого вхождения в слово нет (а, следовательно, вообще нет ни одного вхождения в ), то

считается, что марковская подстановка неприменима к слову .

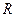Частными случаями марковских подстановок являются подстановки с пустыми словами: , , .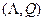

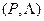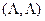Примеры марковских подстановок

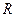
		Результат
логика	(ика, 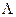)	лог
	(85789, 00)
тарарам	(ара, 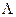)	трам
поляна	(пор, т)	Не применима

Для обозначения марковской подстановки используется запись 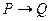. Заключительные подстановки обозначаются .

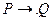Упорядоченный конечный список формул подстановок

в алфавите 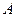называется схемой нормального алгоритма в .

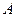Нормальным алгоритмом (Маркова) в алфавите 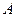называется следующее правило построения последовательности 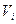слов в алфавите 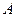, исходя из данного слова в этом алфавите. В качестве начального слова 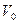последовательности берется слово . Пусть для некоторог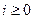о слово 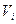построено и процесс построения

рассматриваемой последовательности еще не завершился. Если при этом в схеме нормального алгоритма нет формул, левые части которых входили бы в 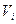, то 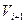полагают равным 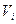и процесс построения последовательности считается завершившимся. Если же в схеме имеются формулы с левыми частями, входящими 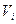, то в качестве 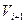берется результат марковской подстановки правой части первой из таких формул вместо первого вхождения ее левой части в слово 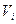; Процесс построения последовательности считается завершившимся, если на данном шаге была применена формула заключительной подстановки, и продолжающимся – в противном случае. Если процесс построения упомянутой последовательности обрывается, то

говорят, что нормальный алгоритм применим к слову .

Последний член последовательности называется результатом применения нормального алгоритма к слову . Говорят, что нормальный алгоритм перерабатывает в .

Функция , заданная на некотором множестве слов алфавита 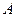, называется нормально вычислимой, если найдется такое расширение 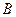данного алфавита (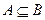) и такой нормальный алгоритм в 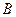, что каждое слово (в алфавите 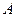) из области определения функции этот алгоритм перерабатывает в слово .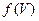

Рассмотрим примеры нормальных алгоритмов.

Пример 1. Пусть 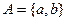- алфавит. Рассмотрим следующую схему нормального алгоритма в :

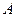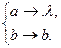
Всякое слово в алфавите 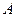, содержащее хотя бы одно

вхождение буквы 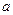, алгоритм перерабатывает в слово, получающееся из исходного слова вычеркиванием в нем самого левого (первого) вхождения буквы 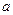. Пустое слово алгоритм перерабатывает в пустое. Алгоритм не применим к словам, которые содержат только букву 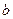. Например,

, , , , .

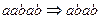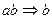Пример 2. Задана функция

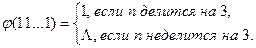
где 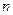- число единиц в слове 11…1.

Рассмотрим схему нормального алгоритма в алфавите .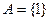

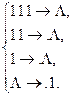
Пока число букв 1 в слове не меньше 3, алгоритм последовательно стирает по три буквы. Если число букв меньше 3, но больше 0, оставшиеся буквы 1 или 11 стираются заключительно; если слово пусто, то оно заключительно переводится в слово 1. Например:

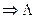1111111 1111 1 ,

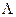
111111111 111111 111 1.

Пример 3. В алфавите 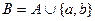, являющемся расширением алфавита 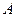, рассмотрим нормальный алгоритм, задаваемый схемой (читается по столбцам).

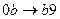
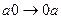
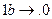
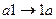
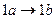
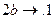
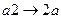
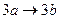
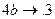
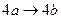
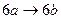
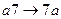
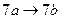
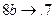
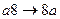
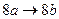
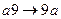
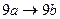
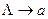
Применим этот алгоритм к слову 3000.

Алгоритм работает следующим образом. На первом шаге применяется самая последняя подстановка: 3000 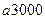. Далее начинают работать подстановки из второго столбца, меняя местами букву 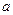с соседними справа цифрами данного числа до тех пор, пока 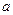не займет крайнее правое положение:

.

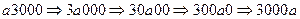Теперь срабатывает одна из подстановок третьего столбца (в данном случае – первая), фактически меняя букву 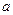на букву 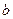: 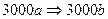. Наконец, срабатывает одна из подстановок первого столбца. Если бы перерабатываемое слово завершилось цифрой, отличной от 0, то сработала бы одна из заключительных подстановок, последняя цифра была заменена цифрой, на единицу меньшей, а алгоритм закончил бы свою работу. В данном случае слово завершается цифрой 0. Поэтому срабатывает подстановка первого столбца: 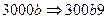. Поскольку и предпоследняя цифра в перерабатываемом слове равна 0, то алгоритм снова применяет первую подстановку, меняя местам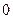и и 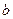и заменяя 0 на 9. Так будет происходить до тех пор, пока левее буквы 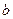не окажется цифра, отличная от 0: 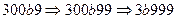. Теперь срабатывает одна из заключительных подстановок: .

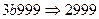А.А. Марков выдвинул гипотезу, получившую название “Принцип нормализации Маркова”. Согласно этому принципу, для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально вычислима.

Сформулированный принцип, так же как и тезисы Тьюринга и Черча, носит внематиматический характер и не может быть строго доказан. Он выдвинут на основании математического и практического опыта.

Рассмотренные три теории (класс всех частично вычислимых функций, класс функций вычислимых по Тьюрингу, класс нормально вычислимых функций), уточняющие понятие алгоритма, оказываются равносильными между собой. Это подтверждается следующей теоремой

Следующие классы функций (заданных на натуральных числах и принимающих натуральные значения) совпадают:

а) класс всех частично рекурсивных функций;

б) класс всех функций, вычислимых по Тьюрингу;

с) класс всех нормально вычислимых функций.

Эта теорема служит косвенным подтверждением адекватности этих теорий опыту вычислений, справедливости каждого из тезисов Тьюринга, Черча и Маркова. Если бы один из этих классов оказался шире какого-либо другого класса, то соответствующий тезис Тьюринга, Черча или Маркова был бы опровергнут. Например, если бы класс нормально вычислимых функций оказался шире класса рекурсивных функций, то существовала бы нормально вычислимая, но не рекурсивная функция. В силу ее нормальной вычислимости она бы была алгоритмически вычислима в интуитивном понимании алгоритма, и предположение о ее нерекурсивности опровергало бы тезис Черча. Но классы Тьюринга, Черча и Маркова совпадают, и таких функций не существует. Это и служит еще одним косвенным подтверждением тезисов Тьюринга, Черча и Маркова.

Контрольные вопросы и упражнения

Задание 1

Дата добавления: 2015-06-27