
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предваренная, сколемовская нормальная и сколемовская стандартная формы
|
|
|
|
Равносильности логики предикатов
Помимо эквивалентностей логики высказываний для логики предикатов справедливы следующие эквивалентности ( ,
, 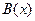 ,
, 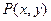 - предикаты, a
- предикаты, a  - высказывание):
- высказывание):
Комбинация кванторов:
1. 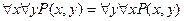 ;
;
2.  ;
;
3. 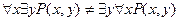 .
.
Комбинация кванторов и отрицаний:
 ;
;
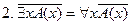 ;
;
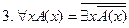 ;
;
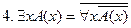 .
.
Расширение области действия кванторов ( не зависит от
не зависит от  ):
):
1.  ;
;
2. 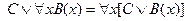 ;
;
3.  ;
;
4. 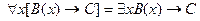 ;
;
5. 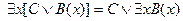 ;
;
6. 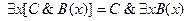 ;
;
7. 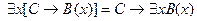 ;
;
8. 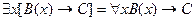 .
.
Расширение области действия кванторов:
1. 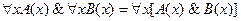 ;
;
2. 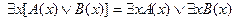 ;
;
3.  ;
;
4. 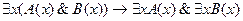 ;
;
5. 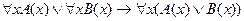 /
/
Нормальная форма. Формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам. Например, для формулы 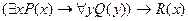 нормальной формой будет
нормальной формой будет 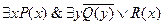 .
.
Предварённая нормальная форма (ПНФ) - нормальная форма, в которой кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики.
Например, для нормальной формы
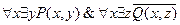 предваренной нормальной формой будет
предваренной нормальной формой будет 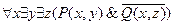 .
.
Всякую формулу логики предикатов можно свести к ПНФ, если использовать следующий алгоритм:
Шаг 1. Исключение логических связок 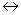 и
и 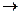 .
.
Шаг 2. Продвижение знака отрицания до атома. Многократно (пока это возможно) делаются замены:
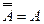 ,
,
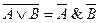 ,
,
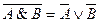 ,
,
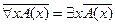 ,
,
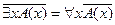 .
.
Шаг 3. Переименование связанных переменных.
Шаг 4. Вынесение кванторов. Для вынесения кванторов используются формулы эквивалентности для исчисления предикатов.
После выполнения четвертого шага получаем ПНФ.
Остановимся более подробно на третьем пункте алгоритма - переименовании переменных.
Пусть 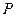 произвольная формула логики предикатов. Формулу
произвольная формула логики предикатов. Формулу 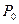 получим из формулы
получим из формулы 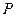 заменой связанных переменных другими переменными, отличными от всех свободных переменных формулы
заменой связанных переменных другими переменными, отличными от всех свободных переменных формулы 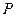 , причем заменяемая переменная в формуле
, причем заменяемая переменная в формуле 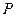 должна меняться одинаковым образом всюду в области действия квантора, связывающего данную переменную, и в самом кванторе. В этом случае
должна меняться одинаковым образом всюду в области действия квантора, связывающего данную переменную, и в самом кванторе. В этом случае 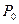 равносильно
равносильно 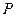 .
.
Таким образом, переименовывать связанные переменные необходимо только в самом кванторе и в области
действия этого квантора. Одинаковые переменные, для которых связывающие их кванторы имеют различные области действия, могут переименовываться разным образом или одна из них может переименовываться, а другая нет.
Пример 1. Пусть имеем формулу  . Нормальная формула имеет вид
. Нормальная формула имеет вид 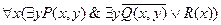 .
.
Переименовываем переменную  в кванторе и в области действия этого квантора на
в кванторе и в области действия этого квантора на 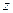 .
.
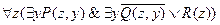 .
.
В полученной формуле переменную  можно переименовать на
можно переименовать на 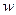 в первой посылке и на
в первой посылке и на 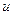 во второй посылке, либо оставить во второй посылке без изменения
во второй посылке, либо оставить во второй посылке без изменения
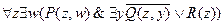 =
=
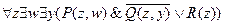
Следующие примеры иллюстрируют применение алгоритма приведения к ПНФ.
Пример 2. 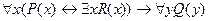 .
.
Шаг 1. 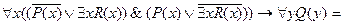
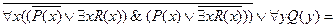
Шаг 2. 
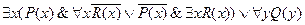 .
.
Шаг 3. 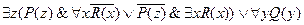
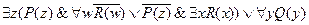 .
.
Шаг 4. Квантор существования 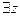 можно вынести за знак дизъюнкции, так как второй член дизъюнкции не зависит от
можно вынести за знак дизъюнкции, так как второй член дизъюнкции не зависит от 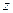 и может рассматриваться как константа.
и может рассматриваться как константа.

Многократно используя этот подход, получаем
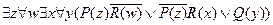 .
.
Пример 3. 
Шаг 1. Так как выражение не содержит операций импликации и эквиваленции, то нет необходимости в первом шаге.
Шаг 2. 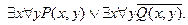
Шаг 3. 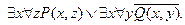
Шаг 4. 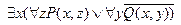 =
=

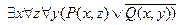 .
.
Можно рассматривать еще более узкий класс формул, так называемых 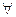 ‑ формул.
‑ формул.
Формула 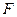 называется
называется 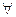 ‑ формулой, если она представлена в ПНФ, причем кванторная часть состоит только из кванторов всеобщности, т.е.
‑ формулой, если она представлена в ПНФ, причем кванторная часть состоит только из кванторов всеобщности, т.е. 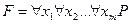 , где
, где 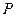 – бескванторная формула. Отсюда возникает задача устранения кванторов существования в формулах, представленных в ПНФ. Это можно сделать путем введения сколемовских функций.
– бескванторная формула. Отсюда возникает задача устранения кванторов существования в формулах, представленных в ПНФ. Это можно сделать путем введения сколемовских функций.
Сколемовская нормальная форма (СНФ) строится в соответствии со следующими правилами:
1. Формула логики предикатов представляется в ПНФ.
2. Последовательно (слева направо) вычеркиваем каждый квантор существования, например 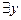 , заменяя все вхождения переменной
, заменяя все вхождения переменной  на новый еще не использованный функциональный символ
на новый еще не использованный функциональный символ 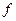 , в качестве аргументов
, в качестве аргументов 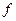 берем все переменные, связанные предшествующими
берем все переменные, связанные предшествующими 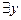 кванторами всеобщности. Функциональный символ
кванторами всеобщности. Функциональный символ 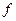 называется сколемовской функцией. Формула логики предикатов, полученная после выполнения шагов 1 и 2, называется сколемовской нормальной формой (СНФ).
называется сколемовской функцией. Формула логики предикатов, полученная после выполнения шагов 1 и 2, называется сколемовской нормальной формой (СНФ).
Пример 1. 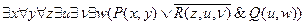
Для получения СНФ вычеркиваем фактор существования 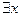 и все вхождения переменной
и все вхождения переменной  заменяем на константу
заменяем на константу 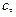 поскольку квантору
поскольку квантору 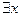 не предшествует ни один квантор всеобщности, то есть сколемовская функция не зависит ни от одной переменной, то есть эта функция является константой.
не предшествует ни один квантор всеобщности, то есть сколемовская функция не зависит ни от одной переменной, то есть эта функция является константой.
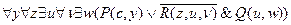
На следующем шаге вычеркиваем квантор существования 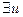 и все вхождения переменной
и все вхождения переменной 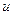 заменяем на функцию
заменяем на функцию 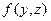
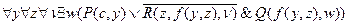 .
.
На последнем шаге вычеркиваем квантор 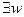 .
.
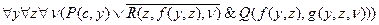 .
.
Переход от ПНФ к сколемовской нормальной форме не затрагивает свойство формулы быть невыполнимой (противоречивой). Это доказывается следующей теоремой.
Теорема. Пусть формула 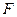 задана в ПНФ и преобразована в СНФ. Тогда
задана в ПНФ и преобразована в СНФ. Тогда 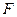 в ПНФ логически невыполнима тогда и только тогда, когда невыполнима СНФ для
в ПНФ логически невыполнима тогда и только тогда, когда невыполнима СНФ для 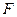 .
.
Однако следует заметить, что если имеется выполнимая формула 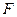 , то может оказаться, что СНФ для
, то может оказаться, что СНФ для 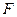 будет невыполнимой.
будет невыполнимой.
Рассмотрим теперь преобразование бескванторной части к виду так называемых дизъюнктов. Дизъюнктом называется формула вида  , где
, где 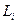 – произвольная литера. Дизъюнкт, не имеющий литер, называется пустым дизъюнктом (ÿ). По определению он всегда ложен.
– произвольная литера. Дизъюнкт, не имеющий литер, называется пустым дизъюнктом (ÿ). По определению он всегда ложен.
Дизъюнкты, соединенные знаком &, образуют КНФ.
Рассмотрим алгоритм равносильного преобразования произвольной бескванторной формулы в КНФ.
Шаг 1. Дана формула 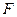 , составленная из литер с применением связок & и Ú. Предполагается, что в формуле исключены скобки между одинаковыми связками, т.е. нет выражений вида
, составленная из литер с применением связок & и Ú. Предполагается, что в формуле исключены скобки между одинаковыми связками, т.е. нет выражений вида 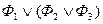 ,
,  ,
, 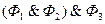 ,
, 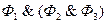 .
.
Шаг 2. Найти первое слева вхождение символов “  (“ или “)
(“ или “)  ” (здесь предполагается, что скобка не является скобкой атома). Если таких вхождений нет, то - формула
” (здесь предполагается, что скобка не является скобкой атома). Если таких вхождений нет, то - формула 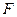 находится в КНФ.
находится в КНФ.
Шаг 3. Пусть первым вхождением указанной пары символов является “  (“. Тогда нужно взять наибольшие формулы
(“. Тогда нужно взять наибольшие формулы 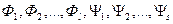 такие, что в
такие, что в 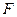 входит формула
входит формула 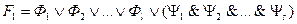 , которая связана с вхождением “
, которая связана с вхождением “  (“. Заменить формулу
(“. Заменить формулу 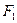 на формулу
на формулу
 &
&

Шаг 4. Пусть первым вхождением является “)  ”. Тогда взять наибольшие формулы
”. Тогда взять наибольшие формулы 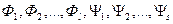 такие, что в
такие, что в 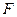 входит формула
входит формула 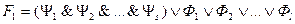 , связанная с вхождением “)
, связанная с вхождением “)  ”. Заменить
”. Заменить 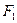 на формулу
на формулу
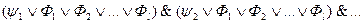
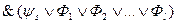 .
.
Шаг 5. Перейти к шагу 2.
Пример. Преобразовать формулу
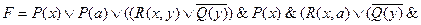
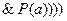 в КНФ.
в КНФ.
Отрабатываем сначала первое, а потом второе вхождение символов “ 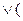 ”.
”.

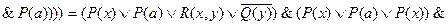
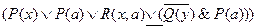 =
=
= 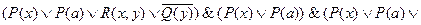

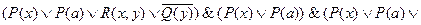
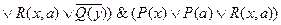 .
.
Здесь чертой подчеркнуты вхождения “ 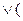 ”. Кроме того, в алгоритме надо предусмотреть приведение подобных членов, а также всевозможные склеивания и поглощения.
”. Кроме того, в алгоритме надо предусмотреть приведение подобных членов, а также всевозможные склеивания и поглощения.
Итак, последовательным применением алгоритма приведения к ПНФ, алгоритма получения СНФ и алгоритма приведения к КНФ с сохранением свойства невыполнимости любая формула 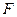 может быть представлена набором дизъюнктов, объединенных кванторами общности. Такую формулу будем называть формулой, представленной в сколемовской стандартной форме (ССФ).
может быть представлена набором дизъюнктов, объединенных кванторами общности. Такую формулу будем называть формулой, представленной в сколемовской стандартной форме (ССФ).
В дальнейшем формулы вида 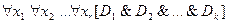 , где
, где 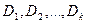 – дизъюнкты, а
– дизъюнкты, а  – различные переменные, входящие в эти дизъюнкты, будет удобно представлять как множество дизъюнктов
– различные переменные, входящие в эти дизъюнкты, будет удобно представлять как множество дизъюнктов 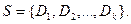
Например, множеству дизъюнктов
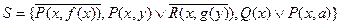
соответствует следующее представление в ССФ
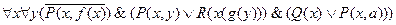
И, наконец, когда говорят, что множество дизъюнктов
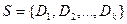 невыполнимо (противоречиво), то всегда подразумевают невыполнимость формулы
невыполнимо (противоречиво), то всегда подразумевают невыполнимость формулы 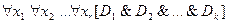 где
где  – различные переменные, входящие в дизъюнкты.
– различные переменные, входящие в дизъюнкты.
Доказательство правильности логического вывода основано на следующих теоремах.
Теорема 1. Даны формулы 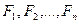 и
и  . Формула
. Формула  является логическим следствием формул
является логическим следствием формул 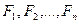 тогда и только тогда, когда формула
тогда и только тогда, когда формула 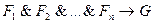 общезначима.
общезначима.
Теорема 2. Даны формулы 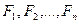 и
и  . Формула
. Формула  является логическим следствием формул
является логическим следствием формул 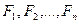 тогда и только тогда, когда формула
тогда и только тогда, когда формула 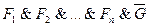 противоречива.
противоречива.
Рассмотрим механизм доказательства правильности умозаключения для логики предикатов на примере
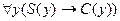 ╞
╞ 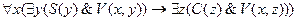 .
.
Воспользуемся второй теоремой. Сначала приведем это выражение к ССФ. Найдем отрицание заключения:
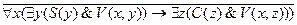 =
=
= 
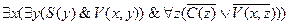 .
.
Перейдем к ПНФ
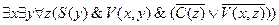 .
.
Получаем СНФ, которая одновременно является и ССФ.
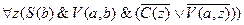 .
.
Формируем произведение
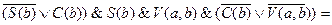 .
.
Контрольные вопросы и упражнения
Задание 1
Какие из следующих выражений являются предикатами. Выделите среди предикатов высказывания.
1. Число  - простое;
- простое;
2. 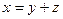 ;
;
3. 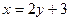 ;
;
4. 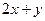 ;
;
5 Все подобные треугольники равны;
6 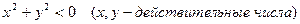 ;
;
7. Все четные числа делятся на число  ;
;
8. Все четные числа делятся на 2;
9. 8 – нечетное число;
10. Имеется бесчисленное множество различных простых чисел;
11. Число 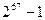 не является простым.
не является простым.
Задание 2
Пусть переменные в нижеследующих выражениях выбираются из множества действительных чисел, а алгебраические знаки имеют свои обычные значения. Определить, истинны ли эти выражения:
1. 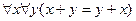 ;
;
2. 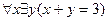 ;
;
3. 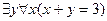 ;
;
4. 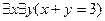 ;
;
5. 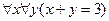 ;
;
6. 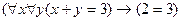 ;
;
7.  ;
;
8. 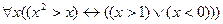 ;
;
9. 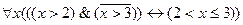 ;
;
10. 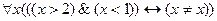 ;
;
11. 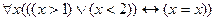 ;
;
12.  .
.
Задание 3
Для действительных чисел записать на языке предикатов предложения, выражающие:
1. коммутативность сложения;
2. коммутативность умножения;
3. ассоциативность сложения;
4. ассоциативность умножения;
5. дистрибутивность умножения относительно сложения.
Задание 4
Выразить области истинности предиката 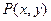 через области истинности предикатов
через области истинности предикатов 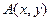 и
и  , если:
, если:
1. 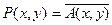 ;
;
2. 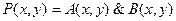 ;
;
3. 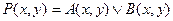 ;
;
4.  ;
;
5. 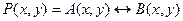 .
.
Задание 5
Указать свободные и связанные переменные:
1. 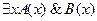 ;
;
2. 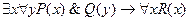 ;
;
3.  ;
;
4.  ;
;
5. 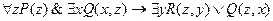 .
.
Задание 6
Пусть все приведенные предикаты определены на множестве действительных чисел. Изобразить графически области изменения свободных переменных, при которых следующие предикаты принимают значение “истина”:
1. 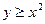 ; 2.
; 2. 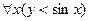 ;
;
3. 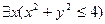 ; 4.
; 4. 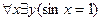 ;
;
5. 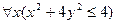 ; 6.
; 6.  .
.
Задание 7
Найти отрицание следующих формул.
1. 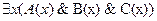 ;
;
2. 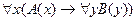 ;
;
3. 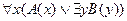 ;
;
4. 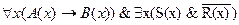 ;
;
5. 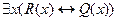 ;
;
6. 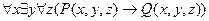 ;
;
7. 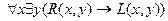 .
.
Задание 8
Привести следующие формулы логики предикатов сначала к предваренной нормальной форме (ПНФ), затем к сколемовской нормальной форме (СНФ) и стандартной сколемовской форме (ССФ).
1. 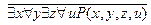 ;
;
2. 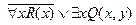 ;
;
3. 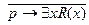 ;
;
4. 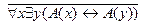 ;
;
5. 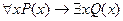 ;
;
6. 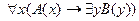 ;
;
7. 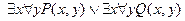 ;
;
8.  ;
;
9. 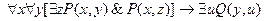 ;
;
10. 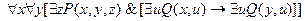 ;
;
11. 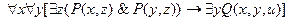 ;
;
12. 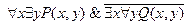 ;
;
13. 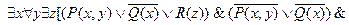
 ;
;
14. 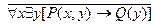 ;
;
15. 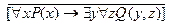 ;
;
16. 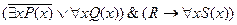 ;
;
17. 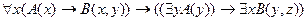 ;
;
18. 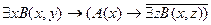 ;
;
19. 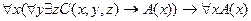 ;
;
20. 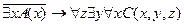 ;
;
21. 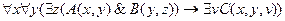 ;
;
22. 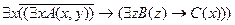 ;
;
23. 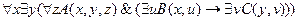 ;
;
24. 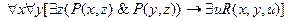 ;
;
25. 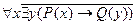 ;
;
26. 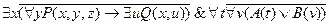 .
.
Задание 9
Пусть  и
и 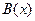 два одноместных предиката, определенных на множестве
два одноместных предиката, определенных на множестве 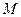 таким образом, что высказывание
таким образом, что высказывание 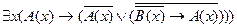 - всегда истинно. Доказать, что высказывание
- всегда истинно. Доказать, что высказывание  - всегда ложно.
- всегда ложно.
Задание 10
Пусть  обозначает “
обозначает “  – простое число”,
– простое число”, 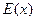 – “
– “  – четное число”,
– четное число”,  – “
– “  – нечетное число”,
– нечетное число”, 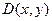 – “
– “  делится на
делится на  ”. Дать словесную формулировку следующим формулам:
”. Дать словесную формулировку следующим формулам:
1. 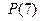 ;
;
2. 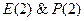 ;
;
3. 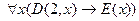 ;
;
4. 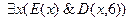 ;
;
5. 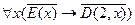 ;
;
6. 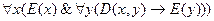 ;
;
7. 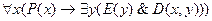 ;
;
8. 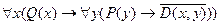 ;
;
9.  ;
;
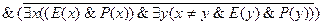 .
.
Задание 11
Даны утверждения 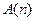 – “число
– “число 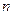 делится на 3”,
делится на 3”, 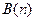 – “число
– “число 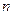 делится на 2”,
делится на 2”, 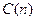 – “число
– “число 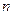 делится на 4”,
делится на 4”,  – “число
– “число 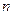 делится на 6”,
делится на 6”, 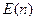 – “число
– “число 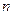 делится на 12”. Укажите, какие из следующих утверждений истины, а какие ложные.
делится на 12”. Укажите, какие из следующих утверждений истины, а какие ложные.
1.  ;
;
2. 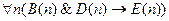 ;
;
3. 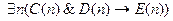 ;
;
4. 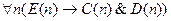 ;
;
5. 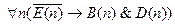 ;
;
6. 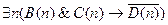 ;
;
7. 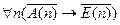 .
.
Задание 12
Доказать следующие равносильности.
1. 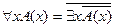 ;
;
2. 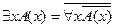 ;
;
3. 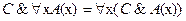 ;
;
4. 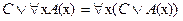 ;
;
5. 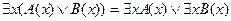 ;
;
6. 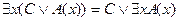 ;
;
7. 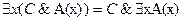 ;
;
8. 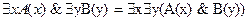 ;
;
9. 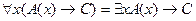 ;
;
10. 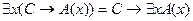 ;
;
11. 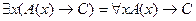 .
.
Задание 13
Какие из заданных формул являются общезначимыми?
1. 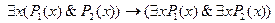 ;
;
2. 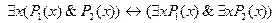 ;
;
3. 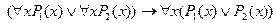 ;
;
4. 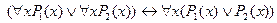 ;
;
5. 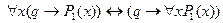 ;
;
6. 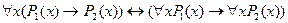 ;
;
7. 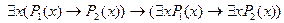 ;
;
8. 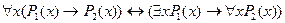 ;
;
9. 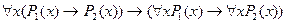 ;
;
10. 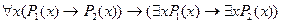 ;
;
11.  ;
;
12. 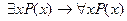 ;
;
13. 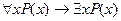 ;
;
14.  ;
;
15. 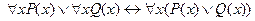 ;
;
16. 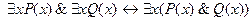 ;
;
17. 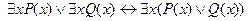 ;
;
18. 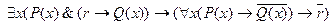 ;
;
19. 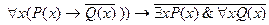 ).
).
Задание 14
Доказать тождественную ложность формул.
 1.
1.  ;
;
2. 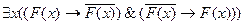 /
/
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 46170; Нарушение авторских прав?; Мы поможем в написании вашей работы!