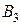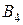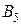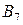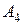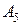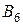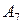КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Направление ЭББ, ЭБТ
|
|
|
|
КР №1. Методы оптимальных решений
(1-10) Дана функция f:
а. Проверить выпуклость функции;
б. Определить стационарную точку;
в. Определить экстремум, если он есть.
1. 
2. 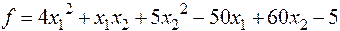
3. 
4. 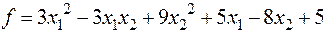
5. 
6. 
7. 
8. 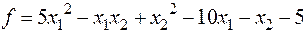
9. 
10. 
(11-20) Даны функция f и ограничения:
а. Составить функцию Лагранжа;
б. Определить стационарную точку;
в. Определить экстремум, если он есть.
11.  :
:
2×x1 – x2 = –2; x1 - 2×x2 = –7; x1 + 2×x2 = 10
12.  :
:
-x1 – 3×x2 = –12; –x1 + 2×x2 = –6; 2×x1 + x2 = 9
13. 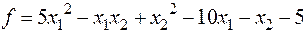 :
:
2×x1 + x2 = –3; –x1 + 2×x2 = 10; –x1 + x2 = –6
14.  :
:
2×x1 – x2 = –2; -x1 + 2×x2 = 7; x1 + x2 = 6
15.  :
:
–x1 + 3×x2 = –10; 7×x1 + 10×x2 = 70; –4×x1 + 5×x2 = 20
16.  :
:
2×x1 - x2 = -2; –x1 + 2×x2 = 7; x1 + x2 = 6
17. 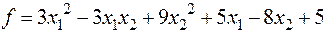 :
:
2×x1 + 3×x2 = 19; –x1 – 3×x2 = 2; 2×x1 – x2 = -1
18.  :
:
2×x1 – x2 = 4; –x1 + x2 = 1; –x1 – x2 = –8
19. 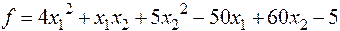 :
:
–x1 + 3×x2 = –6; 7×x1 + 10×x2 = 70; –4×x1 + 5×x2 = 20
20.  :
:
–x1 – 3×x2 = –15; 2×x1 + x2 = 17; –2×x1 – 3×x2 = –23
(21-30) Записать задачу в математической форме, указав экономический смысл вводимых переменных
21. Строительная организация планирует сооружение домов типа Д1, Д2, Д3 с однокомнатными, двухкомнатными и трёхкомнатными квартирами. Один дом Д1 состоит из 10 одно-, 50 двух- и 35 трех- комнатных квартир. Для домов Д2 и Д3 эти данные равны соответственно 20, 60, 10 и 15, 30, 5. Годовой план ввода жилой площади составляет не менее 700 однокомнатных, 2000 двухкомнатных и 600 трёхкомнатных квартир. Требуется составить программу строительства так, чтобы выполнить годовой план с наименьшими затратами, естественно известно, что затраты на возведение одного дома Д1, Д2 и Д3 составляют соответственно 700, 400 и 300 тыс. руб.
22. Для выращивания порции овощей по способу гидропоники необходимо не менее 20 кг питательной смеси, содержащей более 1% фосфора, 1.5% азота, 2% калия и 0.01% различных микроэлементов и не более 1.5% фосфора, 2% азота, 5% калия и 0.03% микроэлементов. Для составления питательной смеси используют 4 вида удобрений. Содержание указанных питательных веществ в 1 кг удобрения первого вида составляет 20, 0, 10, 0 г соответственно, второго – 20, 10, 60, 0.4 г, третьего – 10, 50, 10, 0.5 г, четвертого – 10, 20, 30, 0.2 г. Стоимость 1 кг удобрения каждого вида составляет 7, 6, 8 и 10 рублей соответственно. Сколько килограммов удобрений каждого вида надо взять, чтобы приготовить питательную смесь нужного состава при ее минимальной стоимости?
23. В мастерской при изготовлении столов, шкафов и тумбочек применяются два вида древесины. На один стол расходуется 0.15 м3 древесины первого вида и 0.2 м3 – второго, на один шкаф – 0.2 м3 и 0.1 м3 соответственно, а на одну тумбочку 0.05 м3 древесины первого вида. В наличии имеется 60 м3 древесины первого вида и 40 м3 второго. Количество выпущенных шкафов должно быть не менее 200. Выпуск столов и тумбочек не запланирован. Прибыль мастерской от производства одного стола составляет 12 рублей, шкафа – 15 рублей, тумбочки – 3 рубля. Сколько столов, шкафов и тумбочек должна изготовить мастерская, чтобы получить наибольшую прибыль?
24. Завод выпускает три типа вагонов А, В и С. Строительство вагонов происходит в цехе 1, а производство дополнительных наборов деталей внутреннего оборудования в цехе 2. В первом цехе за плановый период можно построить 25 вагонов А, или 50 вагонов В, или 20 вагонов С. Для цеха 2 эти данные составляют 20, 60 и 30. Прибыль от выпуска одного вагона А составляет 50 рублей, В – 20 рублей, С – 40 рублей. Сколько нужно выпустить вагонов каждого типа за плановый период, чтобы получить наибольшую прибыль?
25. На приобретение оборудования для нового производственного участка имеются капиталовложения 50 тыс. рублей, а для размещения выделена площадь в 74 м2. Можно приобрести оборудование трёх видов. Единица оборудования первого вида занимает 9 м2 и стоит 6 тыс. рублей. Для оборудования 2-ого и 3-ого вида эти данные таковы: 4 м2 и 3 тыс. рублей, 3 м2 и 1 тыс. рублей. Прибыль от единицы нового оборудования составляет 12, 6 и 2 тыс. рублей соответственно. Сколько нужно приобрести нового оборудования каждого вида, чтобы получить наибольшую прибыль и при этом полностью израсходовать выделенные капиталовложения.
26. Студенческая столовая ежедневно готовит три варианта комплексных обедов: мясной по цене 65 рублей, рыбный – по 45 рублей и диетический – по 60 рублей. Суммарное количество реализованных обедов не превосходит 660, из них суммарное количество мясных и рыбных, по крайней мере, в 10 раз больше диетических, а количество мясных, по крайней мере, вдвое больше рыбных. Сколько комплексных обедов каждого варианта должно быть приготовлено, чтобы суммарный кассовый сбор за них бал максимальным?
27. Для изготовления хромоникелевой стали можно использовать два вида руды. Одна тонна руды первого вида содержит в своём составе 2 единицы железа, 1 – хрома, 2 – никеля; для одной тонны руды второго вида содержание этих компонентов составляет 4, 4.5, и 3 соответственно. В сплаве должно содержаться не менее 20 единиц железа, не менее 15 единиц хрома и не менее 10 единиц никеля. Сколько руды каждого вида надо взять для изготовления наиболее дешёвого сплава, удовлетворяющего указанным условиям, если одна тонна руды первого вида стоит 4 денежных единицы, а второго – 10 денежных единиц?
28. Цех выпускает мебель трёх видов. Нормы расходов материалов в м3 на единицу каждого из них составляют 0,032; 0,031; 0,038, нормы времени в н/ч на них равны соответственно 10,2; 7,5; 5,8. Запас материалов на плановый период составляет 90 м3, а фонд рабочего времени – 17000 н/ч. Оптовые цены единицы мебели каждого вида 93 рубля, 67 рублей, 30 рублей, а себестоимость ее изготовления в цехе соответственно 88 рублей, 64 рубля и 29,5 рублей. Плановый ассортимент выпуска мебели составляет 350 единиц, 290 единиц и 800 единиц. Найти план производства, при котором суммарный доход максимален.
29. На выемки породы общим объёмом 900м3 могут быть одновременно использованы три экскаватора А, В, С. Их производительности соответственно равны 10, 15, и 20 м3/ч, а расход горючего за 1ч работы составляет 12л, 20л, 25л. Какой объем работы должен быть выполнен каждым экскаватором при минимальном расходе топлива, чтобы весь объем работ был произведён не более чем за 30ч при условии, что экскаватор С может работать не более 12ч.
30. Архитектурная мастерская планирует застройку района жилыми домами типов Д1, Д2, Д3, состоящих из одно-, двух- и трёх- комнатных квартир. Дом Д1 состоит из 10 одно-, 18 двух- и 20 трёхкомнатных квартир. Для домов Д2 и Д3 эти числа равны 40, 20, 20 и 50, 45, 15 соответственно. В строй необходимо ввести не менее 800 одно-, 1000 двух-, 2000 трёхкомнатных квартир. Составить план застройки района, обеспечивающий минимальную себестоимость строительства, если себестоимость дома Д1 – 830 тыс. рублей, Д2 - 800 тыс. рублей, Д3 - 360 тыс. рублей.
(31-40) Для задачи линейного программирования выполнить следующие действия.
- Записать задачу в матричной форме.
- Записать каноническую задачу.
- Решить задачу геометрически.
- Найти начальный базисный план с помощью искусственных переменных.
- Решить задачу симплекс-методом.
- Написать двойственную задачу к данной задаче в матричной и развёрнутой форме.
- Найти решение двойственной задачи и доказать его оптимальность с помощью теоремы двойственности.
31.  , ,
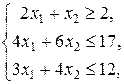

| 36.  , ,
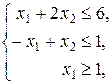

|
32.  , ,
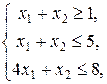

| 37.  , ,


|
33.  , ,


| 38  , ,


|
34.  , ,
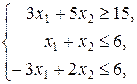

| 39. 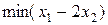 , ,
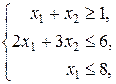

|
35.  , ,
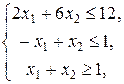

| 40. 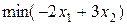 , ,


|
(41-50) Имеется  складских помещений (пунктов отправления)
складских помещений (пунктов отправления)  ,
,  ,…,
,…,  , в которых сосредоточены запасы груза в количествах
, в которых сосредоточены запасы груза в количествах  ,
,  ,…,
,…,  единиц соответственно, и
единиц соответственно, и  пунктов назначения
пунктов назначения  ,
,  ,…,
,…,  , подавших заявки соответственно на
, подавших заявки соответственно на  ,
,  ,…,
,…,  единиц указанного груза. Известна тарифная матрица
единиц указанного груза. Известна тарифная матрица  , в которой
, в которой  – стоимость перевозки одной единицы груза из склада
– стоимость перевозки одной единицы груза из склада  в пункт назначения
в пункт назначения  (
( ;
;  ). Найти план перевозок учитывающий запасы груза на складах и объемы заявок пунктов назначения, имеющий наименьшую общую стоимость. Исходные данные задачи занесены в следующую таблицу
). Найти план перевозок учитывающий запасы груза на складах и объемы заявок пунктов назначения, имеющий наименьшую общую стоимость. Исходные данные задачи занесены в следующую таблицу
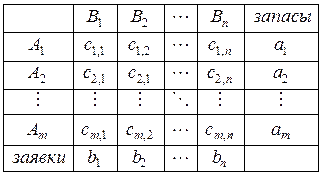
- Построить математическую модель организации перевозок: записать оптимизационную задачу, дать экономическую интерпретацию вводимых переменных.
- Записать двойственную задачу, к построенной задаче линейного программирования.
- Составить начальный план перевозок по методам северо-западного угла и наименьшей стоимости. Укажите стоимости перевозок по этим планам.
- Найти оптимальный план задачи по методу потенциалов и доказать его оптимальность по теореме двойственности.
| 41. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50. |
|
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 2640; Нарушение авторских прав?; Мы поможем в написании вашей работы!