Решение задачи на максимум линейной функции

Рассмотрим пример задачи на поиск оптимального решения в случае максимума линейной функции.

Пример 1. Кондитерский цех выпускает десерты двух сортов: «Наслаждение» и «Лакомка», смешивая три ингредиента: суфле, взбитые сливки и клубничный джем. В таблице 1 приведены нормы расхода ингредиентов, объём запасов каждого ингредиента и прибыль от реализации 1 кг десерта каждого сорта.

Таблица 1. Исходные данные

Ингредиенты	Нормы расхода (кг/кг)	Объем запасов (кг)
Наслаждение	Лакомка
суфле	0,5	0,2
взбитые сливки	0,2	0,6
клубничный джем	0,3	0,2
прибыль от 1 кг (р.)

Требуется составить план производства десертов двух сортов с целью максимизации суммарной прибыли.

Решение. Построим математическую модель задачи.

Пусть x₁ (кг) – количество десерта «Наслаждение», x₂ – количество десерта «Лакомка». Найти значения переменных x₁, x₂, удовлетворяющие условиям:

, (1.1)

при которых целевая функция принимает максимальное значение.

Решение проведем симплексным методом. Приведем систему к каноническому виду введением дополнительных переменных: ,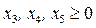

(1.2)

Дополнительные переменные в данной задаче соответствуют остаткам ресурсов. В качестве основных (базисных) переменных выберем дополнительные переменные 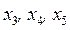. Из каждого уравнения выразим основные переменные через неосновные:

(1.3)

Первоначальное базисное решение является допустимым. Значение целевой функции равно F₀=0.

Значение целевой функции может быть увеличено за счет увеличения значений переменных х₁ и х₂, так как эти переменные входят в линейную целевую функцию с положительными коэффициентами.

На втором этапе решения следует перейти к лучшему (не худшему) решению с помощью смены базиса. В новый базис следует перевести одну из переменных, которая входит в линейную целевую функцию с положительным коэффициентом. Переведем в основные переменные х₁, т.к. в целевой функции коэффициент при ней больше. Число базисных переменных всегда остается постоянным, поэтому одна из переменных старого базиса должна быть переведена в неосновные.

Увеличение значения переменной х₁ приведет к уменьшению переменных старого базиса, т.к. в выражения для этих переменных х₁ входит с отрицательными коэффициентами. Вычислим оценочные отношения для каждой переменной. Для этого разделим свободные члены в каждом выражении на модуль коэффициента при х₁. Если в каком-либо равенстве коэффициент при переменной, переводимой в базис, был бы положительным, то соответствующее оценочное отношение равнялось бы бесконечности (∞).

Оценочные отношения для полученной системы равны соответственно 120, 250, 500/3. Чтобы решение оставалось допустимым (т.е. все переменные оставались неотрицательными) значение х₁ может быть увеличено до наименьшего значения: min{120, 250, 500/3}=120. Уравнение, соответствующее этому оценочному отношению, из которого определяется ограничение на рост переменной х₁, называется разрешающим. Разрешающее уравнение в системе (1.3) подчеркнуто. Следовательно, переменную х₃ переводим в неосновные. Выражая из разрешающего уравнения х₁ и подставляя в остальные уравнения, получим:

(1.4)

Целевая функция примет вид: . Новое базисное решение . Значение целевой функции 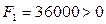. Произошло увеличение значения целевой функции, но в выражении для неё есть переменная х₂ с положительным коэффициентом. Т.е. увеличение переменной х₂ приведет к росту значения целевой функции.

Повторяем процедуру перехода к новому базису. Переведем х₂ в основные переменные. Значение х₂ может быть увеличено до min{300, 50, 175}=50. При этом старые основные переменные останутся неотрицательными. Разрешающее уравнение в системе (1.4) подчеркнуто. Выразим из него х₂ и подставим в остальные уравнения:

(1.5)

Целевая функция примет вид: 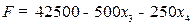. Новое базисное решение 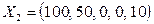. Значение целевой функции . Так как в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то согласно критерию оптимальности для задачи на максимум линейной функции найденное решение является оптимальным.

Таким образом, должно быть произведено 100 кг десерта «Наслаждение» и 50 кг десерта «Лакомка», суммарная прибыль составит 42500 р.

Дополнительные переменные соответствуют неиспользованным ресурсам: ресурсов «суфле» и «взбитые сливки» равны 0, а остатки ресурса «клубничный джем» равны 10 кг.

Дата добавления: 2015-06-27