Решение. 2.1.Для построения модели введем следующие обозначения:

2.1. Для построения модели введем следующие обозначения:

х₁ – объем выпуска продукции А,

х₂ – объем выпуска продукции Б,

S – потребность в трудовых ресурсах,

t – почасовая ставка оплаты труда,

V – размер кредита,

Z – выручка от реализации произведенной продукции,

P – прибыль предприятия.

Выразим в математической форме основные условия и ограничения рассматриваемой задачи.

Ограничения по использованию сырья:

2x1 + 1x2 £ 540;

Ограничения по использованию оборудования:

7x1 + 5x2 £ 2100;

Потребность в трудовых ресурсах S определяется необходимыми затратами труда для выпуска продукции в объемах х₁ и х₂:

S = 8x1 + 1x2.

Размер необходимого кредита определяется, исходя из потребности в трудовых ресурсах S и почасовой ставки оплаты труда t, т.е.

V=tS = t(8x1 + 1x2).

Выручка от реализации произведенной продукции:

Z = 1095x₁ + 520x₂

Сумма расходов по обслуживанию кредита определяется размером возвращаемого кредита и процентов по нему, т.е. равна

40% 3

V + (¾¾ ´ ¾¾¾)V = V + 0.1V = 1.1V.

12 100%

Прибыль предприятия определяется как разность между выручкой и расходами по обслуживанию кредита, т.е.

Р = Z – 1.1V.

Подставляя в эту формулу выражения для Z и V, получим

Р = (1095x₁ + 520x₂)– 1,1 t(8x1 + 1x2) = (1095 – 8,8t)х₁ + (520 – 3,3 t)х₂

Следовательно, математическая модель оптимизации выпуска продукции с привлечением кредитных ресурсов для оплаты труда рабочих принимает следующий вид:

Найти неизвестные значения объемов выпуска х₁, х₂, удовлетворяющих ограничениям

2x1 + 1x2 £ 540

7x1 + 5x2 £ 2100 (1)

х₁³0, х₂³0,

и доставляющих максимальное значение целевой функции:

Р = (1095 – 8,8t)х₁ + (520 – 3,3 t)х₂ → max.

При этом необходимый размер кредита V определяется по формуле:

V = tS = 8tx₁^* + 3tx₂*,

где х₁*, х₂* - оптимальное решение задачи (1). Модель (1) представляет собой задачу параметрического линейного программирования, так как в ее условиях содержится параметр t, от значения которого зависит оптимальное решение.

2.2. При фиксированной ставке оплаты труда t = 10 руб./чел.-час. математическая модель (1) примет вид:

2x1 + 1x2 £ 540

7x1 + 5x2 £ 2100

х₁³0, х₂³0,

Р = 1870х₁ + 627х₂ → max.

Графическое решение задачи изображено на рис. Точкой максимума является точка В с координатами х₁* = 480, х₂*= 540.

Максимальный размер прибыли:

Р* = Р = 1870´480 + 727 ´540= 1290180 (руб.),

Размер необходимого кредита:

V* = 8tx₁^* + 1x2* = 8´10´480 + 3´10´540 =54600 руб.,

Сумма уплаченных процентов: 0,1V* = 0,1´ 54600= 5460руб.

Потребность в трудовых ресурсах: S* = 8x₁^* +3 x₂^* = 8´480 + 3´540 = 5460(чел.-час.).

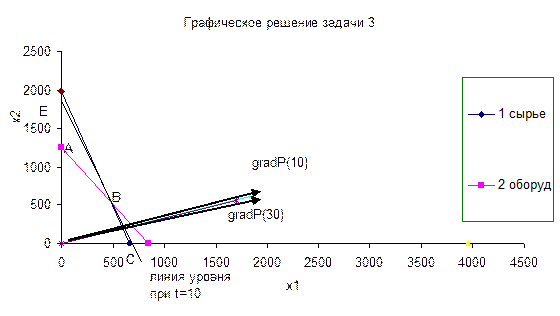
2.3. Потребность в трудовых ресурсах S для обеспечения оптимального выпуска в объемах х₁*, х₂* определяются соотношением:

S* = 8x₁^* + 1x2*,

Но оптимальный план выпуска Х* = (x₁^*, x₂^*), зависит от почасовой ставки t оплаты труда. Следовательно, величина Sтакже зависит от t, т.е. потребность в трудовых ресурсов S есть некоторая функция от параметра t.

Найдем эту функцию. Для этого рассмотрим модель (1) и определим оптимальные планы выпуска Х* = (x₁^*, x₂^*) при различных значениях t, используя графический метод решения задачи линейного программирования.

Пусть t достаточно мало (близко к нулю). Рассмотрим уравнение линии уровня целевой функции

Р = (1095 – 8,8t)х₁ + (520 – 3,3 t)х₂ = h.

При малых значениях t прямая с таким уравнением будет почти параллельна прямой с уравнением

Р = 1095х₁ + 520х₂ = h.

Если «закрепить» линию уровня в т.В и начать увеличивать значение параметра t, то точка Е пересечения линии уровня с осью Ох₂ начнет перемещаться вверх по оси Ох₂ по направлению к точке D.

Найдем значение t, при котором линия уровня параллельна ВС. Из равенства угловых коэффициентов получаем: (1095 – 8,8t)х₁ + (520 – 3,3 t)х₂

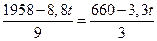, t =20

Следовательно точка B (480;540) остается точкой максимума пока tÎ[0;20).

Найдем максимальный размер прибыли для tÎ[0;20):

Р* = (1095 – 8,8t)´480 + (520 – 3,3 t) ´540 = 1296240-6006t (руб.),

Размер необходимого кредита:

V* = 8tx₁^* + 1x2* = 8´t´480 +3´t´540 =5460t руб.,

Сумма уплаченных процентов: 0,1V* = 0,1´ 5460t = 546t руб.

Потребность в трудовых ресурсах: S* = 8x₁^* + 1x2* = 8´480 +3 ´540 = 5460(чел.-час.).

Если t=20, то оптимальное решение будет достигаться на отрезке ВС, концы которого имеют координаты В(480;540) и C(520;0).

Если «закрепить» линию уровня в т.C и начать увеличивать значение параметра t, то линия уровня будет приближаться к прямой OC.

Найдем значение t, при котором линия уровня параллельна OC. Из равенства угловых коэффициентов получаем:

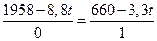; t =200 > 30.

Если tÎ[20; 50] точкой максимума станет точка C(520;0).

Найдем максимальный размер прибыли для tÎ[20;50]:

Р* =(1095-8,8t)´520 +0 = 1292280 – 5808t (руб.),

Размер необходимого кредита:

V* = 8tx₁^* + 3tx₂* = 8´t´520 + 0 =5280t руб.,

Сумма уплаченных процентов: 0,1V* = 528tруб.

Потребность в трудовых ресурсах: S* = 8x₁^* +3 x₂^* = 8´520 + 0 = 5280(чел.-час.).

Итоги решения задачи представим в таблице:

Почасовая оплата труда t (руб.)	Оптималь-ный план выпуска Х*(t)= (x1^*,x2^*)	Величина спроса на трудовые ресурсы S*(t) (чел.-час.)	Размер необходимого кредита V*(t), (руб.)	Величина максимальной прибыли Р*(t) (руб.)
t = 10	(480;540)
tÎ(10;20)	(480;540)		5460t	1296240-6006t
t = 20	Отрезок ВС	[5280;5460]	[105600;109200]
tÎ(20;50]	(520;0)		5280t	1292280 – 5808t

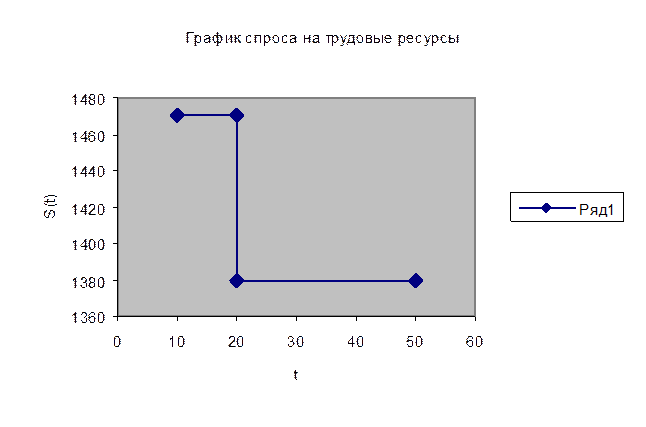
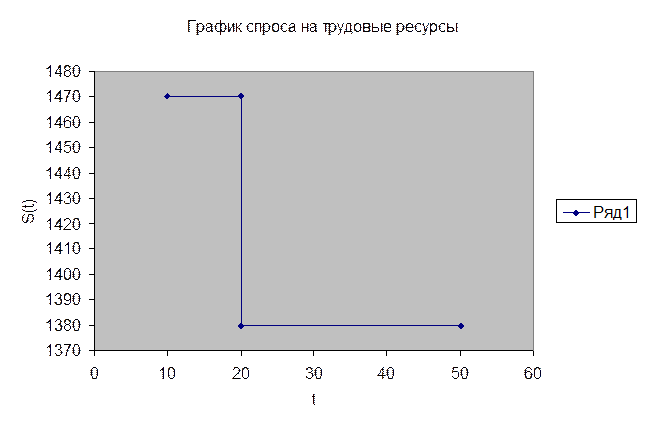
Задача 4

Фирма при производстве продукции использует два вида ресурсов: рабочую силу (L, тыс. чел.-час.) и оборудование (K, тыс. ст.-час.). Производственная функция (ПФ) фирмы, построенная путем обработки статистических данных, имеет вид:

,

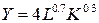где Y — объем выпуска продукции (ед.).

Требуется:

1. Построить графики ПФ при фиксированном значении одной из переменных: а) K = 108; б) L = 36.

2. Найти уравнения изоквант ПФ и построить их графики для Y ₁=133, Y ₂ = 200, Y ₃=267.

3. Известны объем выпуска продукции Y= 200 и наличные трудовые ресурсы L=36 в базовом периоде. Определить потребность в оборудовании в плановом периоде при увеличении объема выпуска продукции на 10%, если возможность увеличения трудовых ресурсов составляет не более 5%.

4. Рабочая сила нанимается по контракту с почасовой оплатой труда 560 (ден.ед./тыс. чел.-час), оборудование берется в аренду с суммарными затратами 80 (ден.ед./тыс. ст.-час). Объем капитала, который фирма может затратить на рабочую силу и оборудование, составляет 32000 (ден. ед.). Построить математическую модель задачи оптимизации выпуска продукции, считая, что ПФ задана на всем множестве K ≥ 0, L ≥ 0; найти графическим методом ее решение. Определить предельную норму технологического замещения оборудования рабочей силой и предельную эффективность финансовых ресурсов в точке оптимума.

Решаем задачу для следующих значений параметров:

А

α

β

К

L

Y1

Y2

Y3

Lбаз

Yбаз

pK

pL

С

0,3

0,7

1) Производственная функция (ПФ) — функция, описывающая зависимость максимального объема производимого продукта от затрат ресурсов (факторов), используемых в производственном процессе. В данной задаче в качестве ресурсов выступают рабочая сила (L, тыс. чел.-час.) и оборудование (K, тыс. ст.-час.). Производственная функция фирмы, построенная путем обработки статистических данных, имеет вид:

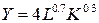
где Y — объем выпуска продукции (ед.).

Построим графики производственной функции при фиксированном значении одной из переменных.

а) По условию K =108. Тогда ПФ — степенная функция следующего вида:

Y = 4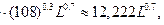

График функции представлен на рис.

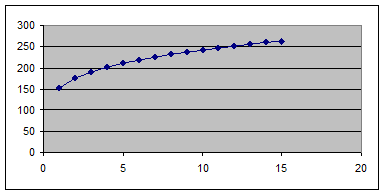
б) По условию L =36. Тогда ПФ — степенная функция следующего вида:

Y =4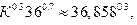

График функции представлен на рис.

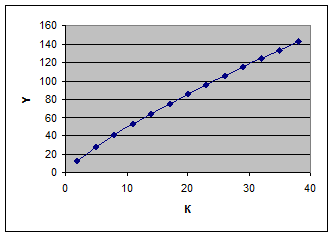
2) Изокванта — совокупность всех комбинаций факторов производства (K, L), обеспечивающих одинаковый объем выпускаемой продукции. Изокванты дают графическое представление двухфакторной производственной функции Y (K, L)в виде ее линий уровня.

По условию Y ₁=133; Y₂ = 200; Y ₃=267.

Выпишем соответствующие этим значениям уравнения изоквант:

Y= 4 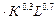=133;

Y= 4 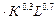=200;

Y= 4 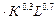=267.

Для построения на декартовой плоскости OKL изоквант из их уравнений в явном виде выразим переменную L как функцию от переменной K:

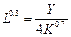или ..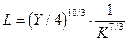

Итак, уравнения трех изоквант запишем в следующем виде:

; ; .

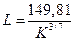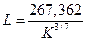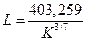Графики изоквант, выпуклые к началу координат кривые, изображены на рис. Различные комбинации (K ₁, L ₁)и (K ₂, L ₂)используемых ресурсов, принадлежащие одной и той же изокванте, дают один и тот же объем выпуска Y. Изокванта Y ₃, расположенная выше изоквант Y ₂ и Y ₁, соответствует большему объему выпуска продукции (Y ₃ > Y ₂ > Y ₁).

		.

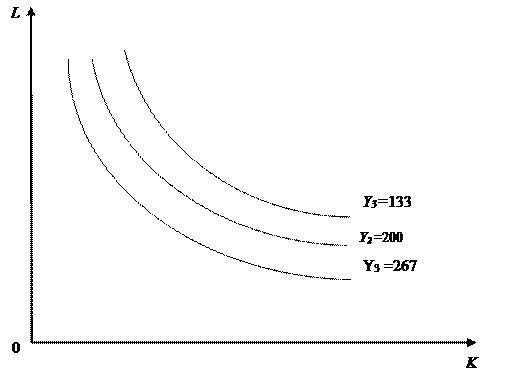3) Известны объем выпуска продукции Y_баз = 200 (ед.) и наличные трудовые ресурсы L_баз =36 (тыс. чел.-час.) в базовом периоде. Определим потребность в оборудовании в плановом периоде при увеличении объема выпуска продукции на 10%, если возможность увеличения трудовых ресурсов составляет не более 5%.

При заданном увеличении объем выпуска продукции составит

Y = 1.1× Y_баз = 1.1×200 = 220 (ед.).

Существует множество комбинаций факторов производства (K, L), обеспечивающих выпуск продукции в объеме 220 ед. Потребность в оборудовании в плановом периоде можно выразить как функцию от объема трудовых ресурсов. Используя уравнение изокванты

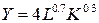=220,

имеем:

.

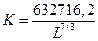Таким образом, если объем трудовых ресурсов, используемых в производстве, не изменится и останется на уровне L_баз =36 (тыс.чел.-час.), то потребность в оборудовании в плановом периоде составит

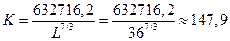(тыс. ст.-час.).

В базовом периоде потребность в оборудовании составляла

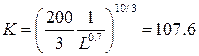(тыс. ст.-час.).

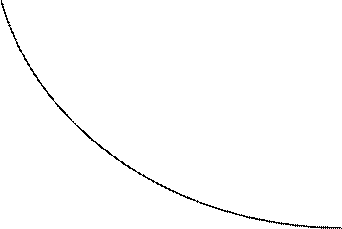Потребность в ресурсах в плановом

периоде:

Если же объем трудовых ресурсов увеличится на 5% по отношению к базовому и составит

L = 1.05× L_баз = 1.05×36 = 37,8 (тыс. чел.-час.),

то потребность в оборудовании в плановом периоде составит

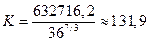(тыс. ст.-час.).

Итак, при объеме трудовых ресурсов 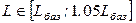потребность в оборудовании в плановом периоде составит некоторую величину 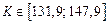, определяемую соотношением

.

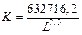4) Согласно условию фирма может приобрести на рынке используемые в производстве ресурсы по ценам p_K = 560 (ден. ед. / тыс. ст.-час.) и p_L = 80 (ден. ед. / тыс. чел.-час.). Величина ее затрат C на покупку L единиц рабочей силы и К единиц оборудования составит

С= p_KК + p_LL = 560 К + 80 L.

Задача фирмы состоит в нахождении максимального объема выпуска продукции при условии, что уровень затрат на покупку ресурсов не превосходит 32000 ден. ед. Математическая модель этой задачи может быть записана так:

найти объемы ресурсов К и L, удовлетворяющие ограничениям

560 К + 80 L ≤ 32000, (1)

К ≥ 0, L ≥ 0 (2)

и доставляющие максимальное значение целевой функции

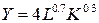→ max. (3)

Так как Y — нелинейная функция, то эта модель представляет собой задачу нелинейного программирования. Ограничение (1) называется бюджетным ограничением.

L

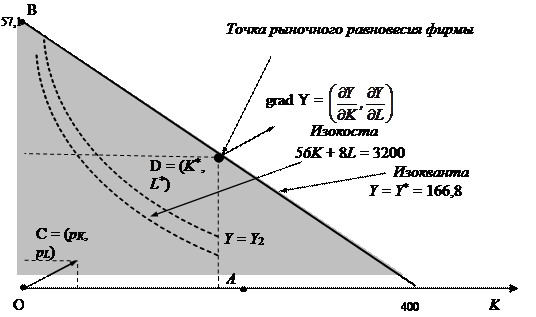Графическое решение задачи производителя

Ее решение можно найти графическим методом. Для этого построим область допустимых решений, задаваемую условиями (1) и (2). Она представляет собой заштрихованный треугольник ОАВ. Граничная прямая АВ бюджетного ограничения задается уравнением

560K + 80 L = 32000

Для определения оптимального решения проведем несколько линий уровня (изоквант) целевой функции, имеющих общие точки с областью допустимых решений. Как было показано в п. 2, чем выше находится изокванта, тем большему уровню целевой функции она соответствует (Y₂ > Y₁). Поэтому изокванта, соответствующая максимально возможному объему выпуска, должна касаться граничной прямой бюджетного ограничения (1), а точка ее касания D будет оптимальным решением задачи.

Для нахождения значений координат точки D используем тот факт, что градиент целевой функции grad Y = 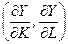, вычисленный в точке касания, перпендикулярен прямой АВ. Это означает, что вектор grad Y и вектор нормали ОС = (p_K, p_L) этой прямой пропорциональны, т.е. справедливо равенство

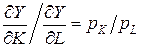. (4)

Поскольку 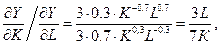отсюда имеем, что

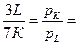
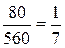
Следовательно, K = 3 L. Подставляя полученное выражение K через L в уравнение граничной прямой АВ, получаем:

80L + 560*3 L = 32000.

Отсюда имеем, что оптимальная величина трудовых ресурсов равна

L^* = 40.

Оптимальный объем оборудования равен

K^* = 4* L = 3*40 = 120,

а соответствующий объем выпуска Y ^* = 4∙120^0.3∙40^0.7 ≈ 166,8.

Предельная норма технологического замещенияоборудования рабочей силойв точке рыночного равновесия равна отношению цен этих ресурсов, т.е.

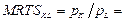1/7.

Предельная эффективность финансовых ресурсов

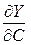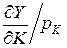= = (0.3∙5∙120^-0.7∙40^0.7)/30 ≈ 0.014,

что означает следующее: при увеличении затрат на 1 ден. ед. объем выпускаемой продукции возрастет на 0.014 ед.

Итак, получены следующие результаты.

1. Фирма должна взять в аренду K ^* = 120 тыс. ст.-час. оборудования и нанять по контракту L ^* = 40 тыс. чел.-час. рабочей силы. В этом случае при имеющемся бюджетном ограничении будет выпущено максимальное количество продукции Y ^* = 166,8ед.

2. Предельная норма технологического замещения оборудования рабочей силой MRTS_KL = 1/7.

Предельная эффективность финансовых ресурсов равна 0.014.

Задача 5

Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме выполнения приведены в следующей таблице:

Имя работы	А	В	С	D	E	F	G	H	Q	V
Опирается на работу	E,Q	G		C,F,H,A		E,Q	V	G	V
Нормальный срок
Ускоренный срок
Норм.стоим.(млн.руб.)	2,1	12,6	25,2	43,4	136,5	47,6	0,7	5,6	107,8
Плата за ускор.(млн.руб.)	3,3	19,8	39,6	68,2		74,8	1,1	8,8	200,2

Требуется:

1. С учетом технологической последовательности работ построить сетевой график выполнения этих работ.

2. Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ. Найти критический путь и его продолжительность, указать все возможные критические пути, определить стоимость всего комплекса работ.

3. Найти минимальное удорожание комплекса работ при сокращении сроков строительства на 2 дн.

Дата добавления: 2015-06-27