Свободные горизонтальные колебания точки

Свободные прямолинейные колебания материальной точки

17.1 Свободные горизонтальные колебания точки.

17.2 Свободные вертикальные колебания груза.

Рассмотрим прямолинейное горизонтальное движение точки М массы m по неподвижной гладкой плоскости под действием упругой силы (рис. 12) 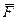пружины.

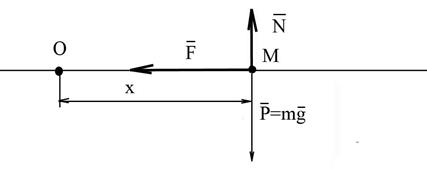
Рис. 12

Начало координат О выберем в положении равновесия точки и направим ось вправо по оси пружины. Пусть М – одно из положений точки в ее движении, возникшем в результате нарушения состояния равновесия. На точку М действуют три силы: сила тяжести 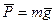, сила реакции 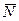гладкой плоскости и упругая сила пружины 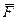. Пусть упругая сила подчиняется закону Гука, т.е ее алгебраическое значение 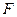пропорционально величине деформации (растяжения или сжатия) пружины

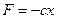
(4.1)

Знак минус означает, что при растяжении пружины (x > 0) имеем 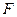< 0, т.е упругая сила направлена в отрицательную сторону оси ; при сжатии - наоборот. Коэффициент пропорциональности , размерность которого н/м, называется жесткостью (упругостью) пружины. Из формулы (4.1) имеем:

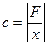
(4.2)

Составим дифференциальное уравнение движения точки М в проекции на ось : или .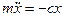

Обозначая 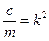, получим:

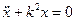
(4.3)

Уравнение (4.3) представляет собой дифференциальное уравнение свободных колебаний материальной точки по гладкой горизонтальной плоскости.

Уравнение (4.3) является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Полагая в уравнении , получим для определения n характеристическое уравнение 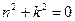. Поскольку корни этого уравнения являются чисто мнимыми 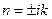, то как известно из теории дифференциальных уравнений, общее решение уравнения (4.3) имеет вид

,

(4.4)

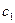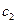где и - постоянные интегрирования. Если вместо постоянных 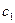и 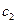ввести постоянные и такие, что 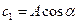, , 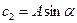то получим или .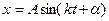

Это другой вид решения уравнения (4.3), в котором постоянными интегрирования являются и .

Колебания, совершаемые точкой по закону (4.5), называются гармоническими колебаниями. Скорость точки

(4.6)

Величина , равная небольшому отклонению точки М от точки О, называется амплитудой колебаний. Величина называется фазой колебаний. Фаза 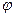, в отличие от координаты определяет не только положение точки в данный момент времени, но и направление ее последующего движения, например из положения М при фазе равной 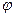, точка движения вправо, а при фазе, равной 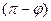, влево. Фазы, отличающиеся на , считаются одинаковыми. Величина определяет фазу начала колебаний (начальная фаза). Например при колебания происходят по закону синуса (начинаются от центра О со скоростью, направленной вправо), при 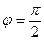- по закону косинуса (начинаются из положения 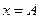со скоростью 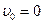). Величина 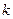называется круговой частотой колебаний .

Промежуток времен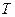и (или ), в течении которого точка совершает одно полное колебание, называется периодом колебаний. По истечению периода фаза изменяется на , откуда период .

Найдем значения и .

Пусть в момент времени 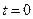точка М находится в положении 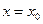и имеет скорость . Подставляя эти значения в (4.5) и (4.6), получим 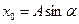, . Отсюда складывая вначале почленно квадраты этих равенств, а затем деля их почленно одно на другое, найдем , .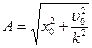

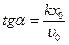Отметим важные свойства свободных колебаний:

1. амплитуда и начальная фаза колебаний зависят от начальных условий;

2. частота 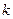, а следовательно и период 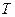колебаний от начальных условий не зависят.

Дата добавления: 2015-06-27