
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения)
|
|
|
|
Пусть на твердое тело, имеющее неподвижную точку 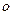 , действуют заданные внешние силы
, действуют заданные внешние силы 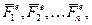 и реакция
и реакция 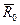 связи (рис. 37).
связи (рис. 37).
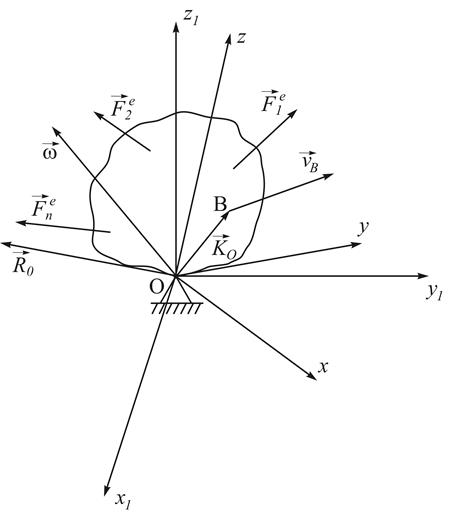
Рис. 37
Чтобы исключить из уравнений движения неизвестную реакцию 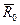 , воспользуемся теоремой об изменении кинетического момента относительно центра
, воспользуемся теоремой об изменении кинетического момента относительно центра 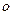 , представив ее в виде (8.4), т.е. в виде теоремы Резаля. Тогда, поскольку
, представив ее в виде (8.4), т.е. в виде теоремы Резаля. Тогда, поскольку  , уравнение (8.4) даст
, уравнение (8.4) даст
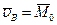
| (8.5) |
где 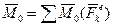 , а
, а 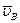 - скорость по отношению к инерциальной системе отсчета
- скорость по отношению к инерциальной системе отсчета 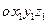 точки
точки 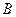 , совпадающей с концом вектора
, совпадающей с концом вектора 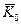 .
.
Движение тела изучается тоже по отношению к инерциальной системе отсчета 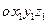 . Но чтобы получить уравнения этого движения в наиболее простой форме проецируем обе части предыдущего равенства на жестко связанные с телом и движущиеся вместе с ним оси
. Но чтобы получить уравнения этого движения в наиболее простой форме проецируем обе части предыдущего равенства на жестко связанные с телом и движущиеся вместе с ним оси 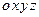 , являющиеся главными осями инерции тела для точки
, являющиеся главными осями инерции тела для точки 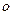 .
.
Тогда выражения проекций вектора 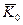 будут иметь простой вид
будут иметь простой вид 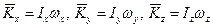 , а входящие в них моменты инерции
, а входящие в них моменты инерции 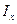
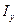
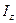 , будут величинами постоянными.
, будут величинами постоянными.
Для вычисления абсолютной скорости 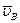 на подвижные оси представим
на подвижные оси представим 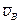 как сумму относительной (по отношению к осям
как сумму относительной (по отношению к осям 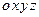 ) скорости
) скорости 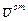 и переносной скорости
и переносной скорости 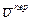 . Тогда из уравнения (8.5)
. Тогда из уравнения (8.5)
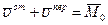 и и 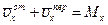 . .
| (8.6) |
Обозначим координаты точки 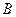 через
через 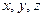 . При этом, так как радиусом – вектором точки
. При этом, так как радиусом – вектором точки 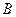 является вектор
является вектор 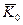 , то
, то 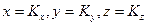 .
.
Как указано в кинематике, при определении 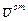 движение осей
движение осей 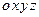 во внимание не принимается, следовательно
во внимание не принимается, следовательно 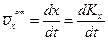 , а при определении
, а при определении 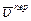 точку
точку 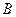 можно рассматривать как принадлежащую телу, связанному с осями
можно рассматривать как принадлежащую телу, связанному с осями 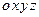 . Но это тело движется вокруг неподвижной точки
. Но это тело движется вокруг неподвижной точки 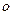 .
.
По аналогии с формулой Эйлера из кинематики 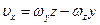 , имеем
, имеем
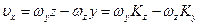
Заменяя в найденных выражениях 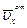 и
и 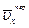 величины
величины 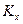 ,
, 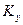 ,
, 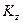 их значениями и подставляя эти значения
их значениями и подставляя эти значения 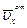 ,
, 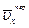 во второе из равенств (8.6), получим
во второе из равенств (8.6), получим
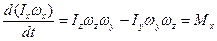
Аналогичные выражения получаются для проекций первого из равенств (8.6) на оси 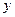 и
и 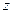 .
.
Так как для связанных с телом осей 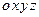 величины
величины 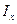
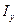
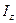 постоянны, то окончательно найдем следующие дифференциальные уравнения движения твердого тела вокруг неподвижной точки в проекциях на главные оси инерции тела для этой точки:
постоянны, то окончательно найдем следующие дифференциальные уравнения движения твердого тела вокруг неподвижной точки в проекциях на главные оси инерции тела для этой точки:
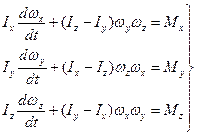
| (8.7) |
Уравнения (8.7) называются динамическими уравнениями Эйлера.
Дифференциальные уравнения движения свободного твердого тела.
Как известно, движение свободного твердого тела слагается из поступательного движения вместе с полюсом, в качестве которого при решении задач динамики выбирают обычно центр масс 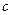 тела, и из движения вокруг центра масс, как вокруг неподвижной точки. Если на тело действуют внешние силы
тела, и из движения вокруг центра масс, как вокруг неподвижной точки. Если на тело действуют внешние силы 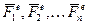 , то движение полюса
, то движение полюса 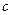 описывается теоремой о движении центра масс
описывается теоремой о движении центра масс 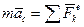 , где
, где 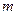 - масса тела.
- масса тела.
В проекциях на неподвижные оси 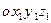 это равенство дает:
это равенство дает:
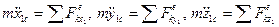
| (8.8) |
где 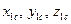 - координаты центра масс тела.
- координаты центра масс тела.
Для движения же вокруг центра масс теорема об изменении кинетического момента дает в проекциях на главные центральные оси инерции тела три уравнения, совпадающие по виду с уравнениями (8.7). Таким образом, система дифференциальных уравнений (8.7), (8.8) описывает движение свободного твердого тела.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 1373; Нарушение авторских прав?; Мы поможем в написании вашей работы!