Уравнения Лагранжа второго рода

Уравнения Лагранжа второго рода предназначены для составления дифференциальных уравнений движения голономных систем довольно общего вида. Если кинетическая и потенциальная энергии системы определены и выражены через обобщенные координаты, то последующие выкладки в уравнениях Лагранжа доведены до автоматизма. Важное достоинство получаемых таким образом уравнений – они не содержат реакций связей (к тому же неизвестных). Но если возникает необходимость определения таких реакций, то метод Лагранжа (путем введения так называемых избыточных координат) позволяет решать и эту задачу.

Будем исходить из общего уравнения динамики:

(9.21)

Возьмем систему с идеальными стационарными связями (уравнения Лагранжа не меняют своей формы и при нестационарных связях), и пусть 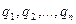- обобщенные координаты системы. Тогда радиус – вектор каждой точки может быть выражен через обобщенные координаты:

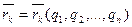
(9.22)

Отсюда находим формулы для вычисления скорости:

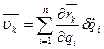
(9.23)

и возможного перемещения:

(9.24)

Нетрудно убедиться в таких тождествах:

(9.25)

Подставляя (9.24) в (9.21), получим:

(9.26)

Здесь - обобщенная сила (как уже известно, из аналитической статики), соответствующая обобщенной координате .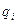

С помощью (9.25) доказывается, что:

,

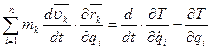где Т – кинетическая энергия системы.

В результате уравнение (9.21) принимает вид:

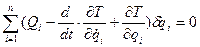
(9.27)

Это уравнение называют общим уравнением динамики в обобщенных координатах. Все вариации в данном уравнении независимы, их можно сообщать поочередно, а потому, как нетрудно видеть, выражения в скобках будут нулями.

Мы приходим, таким образом, к уравнениям Лагранжа второго рода:

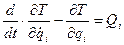
(9.28)

При движении системы в потенциальном силовом поле обобщенные силы выражаются через потенциальную энергию, и уравнения (9.28) принимают вид:

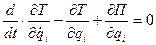
(9.29)

В этом случае их можно представить также в такой компактной форме:

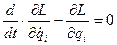
(9.30)

где L = T-M – функция Лагранжа (кинетический потенциал).

Замечание. Обобщенную координату называют циклической, если она не входит явно в функцию L Лагранжа. Нециклические координаты называют позиционными.

Пусть 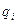– циклическая координата. Для циклических координат уравнения (9.30) принимают вид:

(9.31)

Отсюда следует:

(9.32)

Данные интегралы называют циклическими. Они представляют собой обобщение законов сохранения количества движения и кинетического момента системы.

Примеры.

1. Механическая система состоит из малой и большой призм с массами m и M. Малая скользит по боковой грани большой призмы, которая, в свою очередь, движется по гладкой горизонтальной плоскости под действием заданной силы 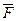. Составить дифференциальные уравнения движения системы. Угол α наклона грани задан.

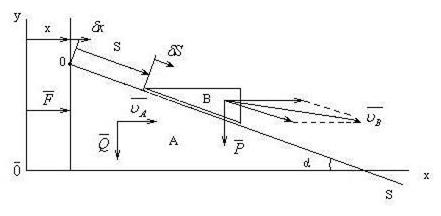
рис. 43.

Применим уравнения Лагранжа в форме (9.28). Рассматриваемая система имеет две степени свободы. За обобщенные координаты примем: х – абсолютное перемещение призмы А; S – относительное перемещение призмы В. Следует раскрыть уравнения:

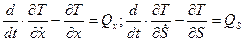
(1)

Замечая, что кинетическая энергия не зависит от координат, а, следовательно,

,

находим левые части уравнений (1):

(2)

Обобщенные силы найдем из выражения элементарной работы, сообщая поочередно элементарные перемещения и . Остановим мысленно призму B на грани призмы A и сообщим всей системе (как твердому телу) перемещение . Получим выражение для элементарной работы 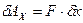. Отсюда следует 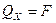. Далее, при остановленной призме А сообщим перемещение малой призме. Получим . Отсюда следует .

Подставляя (2) и выражения для обобщенных сил в (1), получим дифференциальные уравнения движения системы:

2. Составить дифференциальные уравнения колебаний двойного математического маятника. Маятник состоит из двух материальных точек M₁ и M₂ веса и , прикрепленных к концам двух невесомых стержней. Первый стержень может вращаться вокруг неподвижной горизонтальной оси O, а второй – вокруг оси, связанной с точкой M₁.

рис. 44.

Система имеет две степени свободы. За обобщенные координаты примем углы 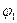и отклонения стержней от вертикали. Для решения задачи воспользуемся уравнениями Лагранжа в форме (9.29). В нашем случае они запишутся так:

(1)

Кинетическая энергия системы равна:

(2)

При составлении выражения потенциальной энергии сил тяжести иногда возникает вопрос о том, в какой точке, на каком уровне принять нулевое значение П. От этого зависит внешняя форма выражения. Но здесь играет роль не П, а 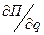. Производная же во всех случаях будет одной и той же.

В рассматриваемой задаче представляется естественным принять П=0 для каждой точки, когда они находятся на оси Ох (в положении равновесия). Если из отклоненного положения возвращать систему на ось Ох, работа сил тяжести будет величиной положительной. А потому:

(3)

Далее вопрос сводится к вычислению производных. Остановимся на координате 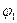. Имеем:

Совершенно аналогично – для координаты .

Окончательную систему запишем в виде:

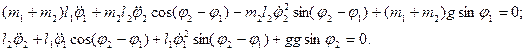
22.5 Принцип Гамильтона – Остроградского

Данный принцип касается в первую очередь, скажем так, философии механического движения. Сущность вопроса состоит в следующем. Представим себе движущуюся механическую систему. Поставим ей в соответствие наглядный геометрический образ – некоторую условную точку, которую назовем изображающей точкой. Это позволяет ввести понятие о траектории изображающей точки (рис. 45). Возьмем на траектории положения A₀ и A₁, соответствующие моментам времени t₀ и t₁. При заданных силах и характере связей можно представить множество путей перехода системы из A₀ в A₁ за время t₁ - t₀. Спрашивается, какой путь выбирает система? Или иначе, какой путь является истинным? Принцип Гамильтона – Остроградского дает ответ на этот вопрос.

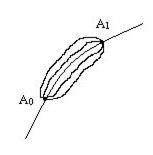
Рис. 45

Вернемся к общему уравнению динамики:

.

(9.33)

Отделим работы сил активных от работы сил инерции и проинтегрируем равенство по времени в пределах от t₀ до t₁:

.

(9.34)

Допустим, что система движется в потенциальном силовом поле. В этом случае элементарная работа сил выражается особенно просто:

Доказывается также, что .

Таким образом, равенство (9.34) приводится к виду:

,

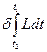(9.35)

где L = T – П – кинетический потенциал.

Интеграл называют действием по Гамильтону.

Окончательно, принцип Гамильтона – Остроградского:

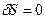
(9.36)

Принцип утверждает: действие по Гамильтону S имеет стационарное значение на истинном пути системы, если к сравнению с ним привлекается многообразие окольных путей, совпадающих с истинным в начальный и конечный моменты времени t₀ и t₁.

Если интервал времени t₁ - t₀ достаточно мал, действие S имеет минимум. [Четаев].

Дата добавления: 2015-06-27