Введение. Начала аналитической механики

Начала аналитической механики

Аналитическую механику отличает общность аналитических методов постановки и решения задач механики. Будь то составление уравнений равновесия или движения механических систем, разыскание возможных положений равновесия или законов движения, исследование устойчивости равновесия или движения и т.д.

Основы аналитической механики были разработаны Ж. Лагранжем. В своем курсе, вышедшем в 1788 году он писал: «В этой работе совершенно отсутствуют какие бы то ни было чертежи. Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений; они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу. Все любящие анализ с удовольствием убедятся в том, что механика становится новой отраслью анализа, и будут мне благодарны за то, что этим путем я расширил область его применения».

В основе аналитической механики лежат понятия связи, возможного перемещения и возможной работы. Определения, важные для последующего изложения, поясним, прибегнув к простому примеру.

Возьмем математический маятник – рис 38.

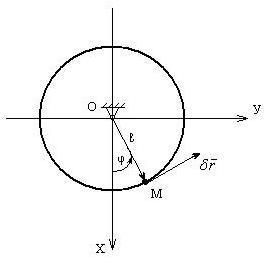
рис.38

Материальная точка с помощью безмассового жесткого стержня подвешена к центру вращения О. Понятно, что точка М несвободна. Её движение подчинено условию:

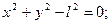
(9.1)

Данное условие является уравнением голономной (ограничения наложены на координаты (х, у) точки и на её положение), удерживающей (точка М не может ни удалиться от центра О, ни приблизиться к нему), стационарной (время t явно не входит в уравнение (9.1)) связи.

Если стержень заменить нитью, получим голономную, стационарную, неудерживающую связь (точка М не может удалиться от центра О, но может приближаться к нему). Неудерживающие связи записываются в виде неравенств. Наконец, если длина нити будет переменной, зависящей от времени l = l(t), связь будет голономной, неудерживающей, нестационарной. Есть вид связей, называемых неголономными, которые накладывают ограничения на скорости точек системы. В нашем курсе системы с такими связями не рассматриваются.

Продифференцируем уравнение (9.1) по времени:

.

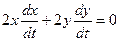Отсюда, заменив символ d на δ, получим:

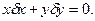
(9.2)

Это условие называют варьированным уравнением связи. Оно накладывает ограничение, как на координаты, так и на приращения (вариации) координат.

Условие (9.2) можно представить в форме:

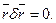
(9.3)

где 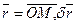- возможное (элементарное) перемещение точки М. Возможным перемещением точки называют бесконечно малое, воображаемое перемещение, совместимое со связями. Из (9.3) видно, что возможное перемещение точки М направлено по касательной к траектории.

Мы определили положение точки М с помощью координат x, y и ввели уравнение связи. Можно поступить иначе. Учтя связь, сразу определить положение точки М с помощью координаты (угла) 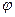. Координаты, при введении которых непосредственно учитываются связи, называют обобщенными координатами. В голономной системе число обобщенных (независимых) координат равно числу степеней свободы.

Предположим, что на точку М действует система 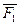, , …, активных сил. Помимо них к точке приложена реакция 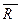связи (стержня). Возможной (элементарной) работой активных сил называют алгебраическую величину:

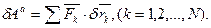
(9.4)

Аналогично – для реакции связи: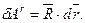

Но поскольку 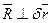, то 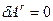. Связь в нашем случае является идеальной. Связи называются идеальными, если возможная работа их реакции на любом возможном перемещении системы равна нулю.

Дата добавления: 2015-06-27