Элементарная теория гироскопа

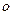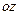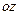Гироскопом называют симметричное твердое тело совершающее движение вокруг неподвижной точки , расположенной на оси симметрии . Ось гироскопа, как ось симметрии, является одновременно его главной центральной осью инерции. Простейшим примером гироскопа является детский волчок. В гироскопических приборах ротор гироскопа обычно закрепляют в кардановом (кольцевом) подвесе, позволяющем ротору совершить любой поворот вокруг неподвижного центра подвеса 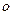, совпадающего с центром тяжести ротора. Такой гироскоп, как и волчок имеет три степени свободы.

У гироскопов, применяемых в технике, угловая скорость 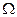(омега) вращения гироскопа вокруг оси 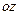больше угловой скорости , которую может иметь сама ось 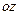при ее повороте вместе с гироскопом вокруг точки 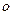, в десятки и сотни тысяч раз (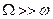), что позволяет построить весьма эффективную приближенную теорию гироскопа, называемую элементарной или прецессионной. Исходят при этом из следующего.

В каждый момент времени абсолютная угловая скорость гироскопа 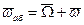, а его движение, как движение тела, имеющего неподвижную точку, слагается из серии элементарных поворотов с этой угловой скоростью 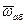вокруг мгновенных осей вращения 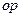(рис. 35)

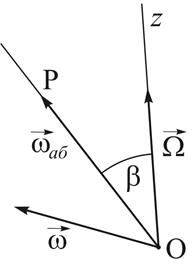
Рис. 35

Но когда 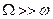, угол 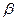между векторам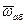и и 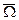очень мал и практически можно принять, что 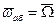, а ось 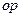в любой момент времени совпадает с осью 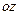гироскопа. Тогда кинетический момент 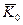гироскопа относительно точки 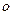можно тоже считать в любой момент времени направленным вдоль оси 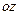и численно равным 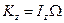. В этом и состоит основное допущение элементарной теории гороскопа. Таким образом, в дальнейшем будем считать 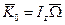, где 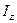- момент инерции гироскопа относительно его оси 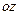, а саму ось 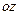и вектор 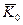полагать все время направленным вдоль одной и той же прямой.

Исходя из элементарной теории, установим каковы основные свойства гироскопа.

1. Свободный трехстепенной гироскоп

Рассмотрим гироскоп с тремя степенями свободы, закрепленный так, что его центр тяжести неподвижен, а ось может совершать любой поворот вокруг этого центра. Такой гироскоп называют свободным. Для него, если пренебречь трением в осях подвеса, будет

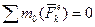и 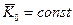, т.е. модуль и направление кинетического момента гироскопа постоянны. Но так как направления вектора 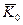и оси 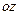гироскопа все время совпадают, то следовательно и ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной системе отсчета. Это одно из важных свойств гироскопа, используемое при конструировании гироскопических приборов.

2. Действие силы (пара сил) на ось гироскопа. Устойчивость оси гироскопа.

Пусть на ось гироскопа начинает действовать сила 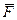, момент которой относительно центра 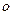равен 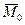(или пара сил 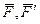с моментом равным 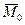) (рис. 36).

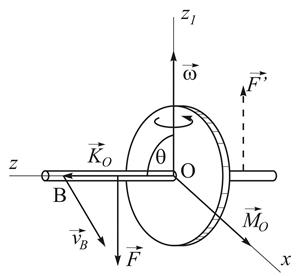
Рис. 36

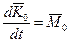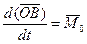Тогда по теореме об изменении кинетического момента или , где 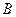- точка оси, совпадающая с концом вектора 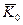. Отсюда, учитывая, что производная от вектора 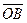по времени равна скорост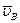и точки 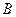, получаем

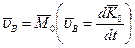
(8.4)

Равенство (8.4) выражает теорему Резаля: скорость конца вектроа кинетического момента тела относительно центра 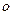равняется по модулю и направлению главному моменту внешних сил относительно того же центра. Следовательно точка 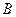, а с нею и ось гироскопа, будет перемещаться по направлению вектора 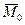. В результате находим, что если на ось быстро вращающегося гироскопа действует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор 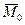момент этой силы относительно неподвижной точки 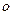гироскопа, т.е. перпендикулярно силе. Аналогичный результат имеет место и при действии на ось гироскопа пары сил.

Из равенства (8.4.) следует, что когда действие силы прекратится, то 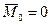, а следовательно и 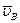обращается в нуль и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменяет своего направления. В этом проявляется свойство устойчивости оси быстро вращающегося гироскопа.

3. Прецессия гироскопа.

Допустим, что сила 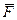(или пара сил 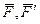) действует на гироскоп во все рассматриваемое время его движения, оставаясь в плоскости 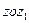(такой силой может, например, быть сила тяжести). Так как по установленному выше ось 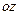в сторону действия силы не отклоняется, то угол 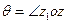остается все время постоянным, а скорость 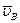- перпендикулярной плоскости .

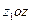Следовательно, ось гироскопа 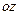будет вращаться (прецессировать) вокруг оси 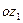с некоторой угловой скоростью 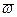, называемой угловой скоростью прецессии. Найдем уравнение, определяющее . Так как ось 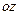вращается вокруг оси 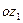с некоторой угловой скоростью 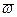, то по формуле вектора скорости точки 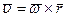, где

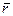- радиус – вектор точки, имеем 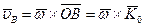и равенство (8.4.) дает

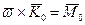
Это уравнение является исходным приближенным уравнением элементарной (прецессионной) теории гироскопа. Из него следует, что 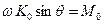, откуда

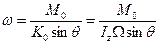
Чем больше 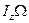, тем меньше и тем большую точность дает элементарная теория.

Дата добавления: 2015-06-27