Дифференциальные уравнения поступательного движения твердого тела

Приложение теорем динамики системы к динамике твердого тела

21.1 Дифференциальные уравнения поступательного движения твердого тела. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

21.2 Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси.

21.3 Дифференциальные уравнения плоскопараллельного (плоского) движения твердого тела.

21.4 Элементарная теория гироскопа.

21.5 Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения). Дифференциальные уравнения движения свободного твердого тела.

При поступательном движении твердого тела все его точки движутся так же, как и центр масс, поэтому дифференциальные уравнения движения центра масс тела являются дифференциальными уравнениями поступательного движения твердого тела:

Здесь 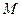- масса тела;

-координаты центра масс тела;

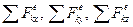-проекции внешних сил на оси координат.

По дифференциальным уравнениям поступательного движения можно решать два основных типа задач на поступательное движение твердого тела.

1) по заданному движению твердого тела определять главный вектор приложенных к нему внешних сил и

2) по заданным внешним силам, действующим на тело и начальным условиям движения находить кинематические уравнения движения тела.

Изучение поступательного движения твердого тела, таким образом, сводится к изучению движения отдельной материальной точки, имеющей массу этого тела.

Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси с угловой скоростью (рис.32)

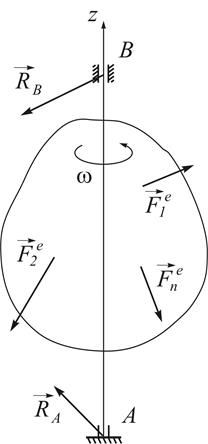
Рис. 32

Кинетический момент данного тела относительно оси будет

Реакции и подпятника 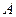и подшипника B являются внешними силами, но их моменты относительно оси равны нулю. Тогда по теореме об изменении кинетического момента системы 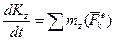, получим , 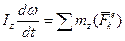или

Таким образом,

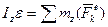
(8.1)

Уравнение (8.1) представляет собой дифференциальное уравнение вращательного движения твердого тела: произведение момента инерции тела относительно оси вращения на угловое ускорение равно алгебраической сумме моментов внешних сил относительно оси.

Дата добавления: 2015-06-27