Примеры. Введем координатную ось As

1. Задача Н.Е. Жуковского. Однородный брусок длины l и массы M опирается на гладкий пол и гладкую стену. По бруску сбегает акробат, масса которого m. Спрашивается, как, по какому закону должен бежать акробат (если принять его за материальную точку), чтобы брусок оставался неподвижным? Угол θ наклона бруска к полу задан.

Введем координатную ось As. Пусть s – координата материальной точки,

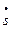- скорость; тогда произведение m 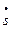будет количеством движения всей системы (поскольку брусок неподвижен).

Рис. 28

Реакции пола и стены проходят через точку О, которая также остается неподвижной. Запишем теорему об изменении кинетического момента системы относительно точки О:

.

Отсюда находим дифференциальное уравнение движения:

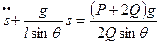. (1)

Как видим, акробат должен бежать по тому же закону, по какому движется материальная точка такой же массы под действием постоянной силы

,

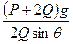направленной в положительную сторону оси As, и переменной силы

,

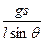подобной силе упругости пружины жесткости 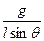, направленной к началу координат. Уравнение (1) имеет общее решение:

.

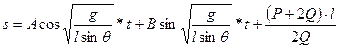При нулевых начальных условиях акробат должен бежать по закону:

,

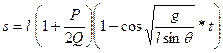2. Карусель может вращаться без трения вокруг вертикальной оси Az. На карусели стоит человек. В некоторый момент времени он начинает идти по окружности радиуса R со скоростью 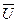(относительно карусели). Определить угловую скорость ω вращения карусели, если масса человека m, а момент инерции карусели .

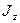Внешними силами, действующими на систему, являются силы тяжести и реакции подшипников. Так как силы тяжести параллельны оси вращения, а реакции пересекают эту ось, то сумма моментов

.

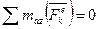Следовательно, имеет место закон сохранения кинетического момента

.

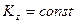Но в начальный момент система находилась в покое, так что равенство 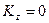выполняется при любом времени.

Пусть 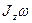- кинетический момент карусели, 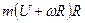- кинетический момент человека. Кинетический момент системы:

.

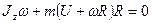Отсюда находим угловую скорость вращения карусели:

.

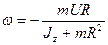Знак минус свидетельствует о том, что карусель будет вращаться в направлении, противоположном показанном на рисунке.

Дата добавления: 2015-06-27