Вводные определения и дифференциальные уравнения движения

Общие теоремы динамики системы

Системой материальных точек или механической системой, или просто системой называют совокупность материальных точек, движения которых взаимно зависимы. Неизменяемую систему точек называют абсолютно твердым телом. Система может состоять из совокупности твердых тел.

Систему называют свободной, если для ее точек возможны всякие движения, и называют несвободной, если есть некоторые ограничения, так что не всякие движения (положения) точек становятся возможными. Эти ограничения, стесняющие свободу движения, называют связями.

В динамике системы различают силы внешние и внутренние. Внешние – это воздействия на систему сторонних объектов, внутренние – силы взаимодействия между отдельными точками системы. Как те, так и другие могут быть задаваемыми и реакциями связей. Силы реакций исчезают вместе с исчезновением связей. При этом задаваемые остаются.

Представим себе движущуюся систему из N материальных точек. Пусть - массы точек. Обратим внимание на точку Mk. (рис. 25)

Рис. 25

Здесь: - равнодействующие внешних и внутренних сил, - скорость и ускорение точки, , , - радиусы-векторы, смысл которых виден непосредственно из рисунка, О – неподвижный центр, С – центр масс системы.

Центром масс системы называют геометрическую точку, положение которой определяется равенством:

(7.1)

где - масса системы.

Если в (7.1) обе части умножить на g (ускорение тяжести), то вместо масс будем иметь силы тяжести. Следовательно, при одинаковых для всех точек системы ускорениях g центр масс совпадает с центром тяжести. Отнеся (7.1) к координатной системе, получим координаты точки С.

и две других координаты.

Продифференцируем в (7.1) обе части по времени (последовательно два раза), получим:

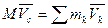, (7.2)

где 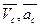- скорость и ускорение центра масс. Равенства (7.2) играют важную роль в динамике системы.

Теперь запишем основной закон динамики для каждой материальной точки. Таким образом мы придем к дифференциальным уравнениям движения системы в векторной форме:

(7.3)

В проекциях будем иметь 3N уравнений в скалярной форме:

Здесь важно иметь в виду основное свойство внутренних сил: их главный вектор и главный момент (в силу третьего закона Ньютона) равны нулю, т.е.:

(7.4)

Но это не означает, что внутренние силы не влияют на движение материальных точек системы. Например, когда акробат находится в свободном полете, отдельные части его тела могут производить довольно замысловатые действия. Они выполняются внутренними силами. В то же время центр масс акробата движется по параболе, и это движение не подвержено влиянию внутренних сил.

Важными следствиями уравнений (7.3) являются общие теоремы динамики, которыми устанавливаются зависимости между некоторыми суммарными мерами движения системы и суммарными мерами действия приложенных сил. Таких теорем четыре: об изменение количества движения, о движение центра масс, об изменении кинетического момента и об изменении кинетической энергии. Первые три теоремы замечательны тем, что позволяют исключить из динамических соотношений внутренние силы; последняя позволяет исключить силы, не совершающие работы при перемещениях точек системы.

Дата добавления: 2015-06-27