Теорема об изменении кинетического момента

Как уже сказано, данная теорема определяет закон вращения системы. Вернемся к рис. 25 и назовем кинетическим моментом системы относительно точки О векторную величину:

, (7.11)

где - кинетический момент относительно центра масс. Подобно тому как в динамике одной материальной точки запишем теорему моментов для точки , входящей в систему.

.

Просуммировав по всем точкам и приняв во внимание свойство внутренних сил, получим окончательно:

(7.12)

Производная по времени от кинетического момента системы относительно неподвижного центра равна главному моменту внешних сил.

Представим (7.11) в виде:

Отсюда, как нетрудно показать, следует теорема для относительного движения:

(7.13)

Здесь кинетический момент и момент сил вычисляются относительно центра масс. Теорема формулируется как и в предыдущем случае. Если в (7.12) или (7.13) правую часть обратить в нуль, то придем к законам сохранения кинетического момента, заключающегося в неизменности вектора 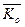или .

Формулой (7.12) удобно пользоваться, когда движение системы представляется как одно вращение вокруг некоторого центра, например, в динамике твердого тела с одной неподвижной точкой. Формула (7.13) более удобна, когда движение системы представляется как сложное, состоящее из поступательного и вращения; например, в динамике самолета, автомобиля и т.д. Уравнение вращения самолета в полете было бы неудобно записывать относительно точки, которая находиться на земле.

Спроектируем (7.12) на направление Оz, получим теорему в скалярной форме:

Отсюда, в случае , находим закон сохранения:

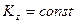
Если внешние силы не создают вращающего момента вокруг оси Оz, то кинетический момент системы относительно этой оси остается неизменным.

Дата добавления: 2015-06-27