
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
|
|
|
|

Рис. 33
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси 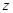 под действием приложенных к нему внешних задаваемых сил
под действием приложенных к нему внешних задаваемых сил 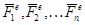 . Пусть тело, в рассматриваемый момент имеет угловую скорость
. Пусть тело, в рассматриваемый момент имеет угловую скорость 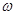 и угловое ускорение
и угловое ускорение  . Так как
. Так как 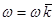 , то
, то  (рис. 33).
(рис. 33).
Составим вначале суммы проекций на координатные оси сил инерции. Проведем для точки  радиус – вектор
радиус – вектор  .
.
Рассмотрим произвольную точку  тела. Для нее сила инерции
тела. Для нее сила инерции  , где
, где  - касательная сила инерции;
- касательная сила инерции;
 - нормальная сила инерции.
- нормальная сила инерции.

|
Так как  , то
, то

|
В проекциях на оси координат:
 , ,  , , 
| (а) |
 . Так как
. Так как
 , то , то
|
 .
.
В проекциях на оси координат:
 , , 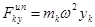 , , 
| (б) |
Суммируя равенства (а) и (б), получим:


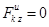
|
По определению координат центра масс
 ,
,  , где
, где
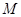 - масса тела.
- масса тела.
Тогда
 , , 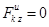 . .
| (в) |
Найдем сумму моментов сил инерции относительно координатных осей.
 , , 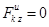 . .
|

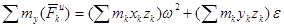

 , так как линии действия этих сил проходят через ось , так как линии действия этих сил проходят через ось 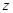 . .
|
Тогда
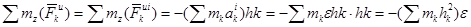
|
Так как  ,
, 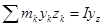 - центробежные моменты инерции, а
- центробежные моменты инерции, а
 - момент инерции тела относительно оси
- момент инерции тела относительно оси 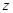 , то
, то

| (г) |
Расстояние  между подпятником
между подпятником 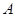 и подшипником
и подшипником 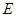 обозначим
обозначим  .
.
Согласно принципа Даламбера заданные силы, силы реакций и силы инерции находятся в равновесии в любой момент времени. Составим для этой системы сил шесть уравнений равновесия с учетом равенств (в) и (г):

| (8.2) |
Установим условия, при которых динамические составляющие реакций подшипников равны нулю. Чтобы получить эти условия, приравняем нулю сумму членов, зависящих от сил инерции в каждом из уравнений

|
Решая эту систему относительно  и
и 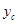 , получим
, получим 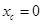 ,
,  ,
,
т.е. устанавливаем, что центр тяжести тела должен находиться на оси его вращения.

|
Решая эту систему относительно  и
и 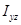 , получим
, получим 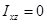 ,
, 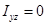 это означает, что ось вращения
это означает, что ось вращения 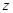 тела должна быть главной осью инерции тела для начала координат.
тела должна быть главной осью инерции тела для начала координат.
Таким образом установлено, что динамические составляющие реакций подпятника и подшипника равны нулю в том случае, если ось вращения тела является главной центральной осью инерции тела.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 4228; Нарушение авторских прав?; Мы поможем в написании вашей работы!