Примеры. 1. Платформа массы М стоит на рельсах

1. Платформа массы М стоит на рельсах. На ней находиться человек массы m, который также неподвижен. В некоторый момент человек начинает перемещаться по платформе со скоростью 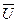(относительно платформы). Определить скорость 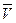платформы. Трением колес о рельсы пренебречь.

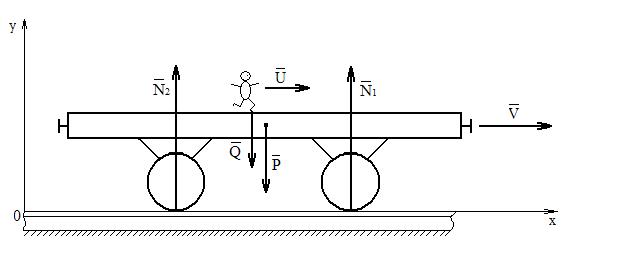
Рис. 26

Изобразим все внешние силы, действующие на систему. Это будут силы тяжест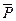и и 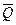и нормальные реакции 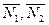рельсов. Очевидно, что 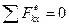. Следовательно, по направлению оси Ох выполняется закон сохранения количества движения. В начальный момент количество движения системы равно нулю. Оно останется нулем и в другое последующее время. Для текущего времени 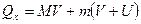. В силу закона сохранения:

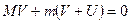
Отсюда находится скорость платформы:

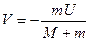
Знак минус свидетельствует о том что, когда человек пойдет направо (согласно рисунку), платформа будет уходить влево. При этом колеса вращаться не будут, и платформа не будет отличаться от саней.

2. Электродвигатель установлен свободно на горизонтальной шероховатой плоскости. Дано: 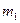- масса станины, 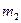- масса ротора, ω - угловая скорость вращения

ротора (постоянная), АВ=s - смещение центра масс ротора относительно оси вращения вала. Выяснить условия, при которых возможны перемещения двигателя по плоскости и его подпрыгивание.

Рис. 27

Изображаем все действующие на систему силы: задаваемые 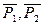и реакции плоскости 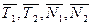. Применительно к нашей задаче записываем теорему о движении центра масс:

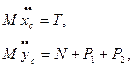(1)

где 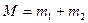- масса системы, , .

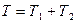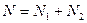По определению центра масс имеем равенства:

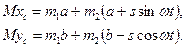
Отсюда, приняв во внимание, что а и b – постоянные, получим:

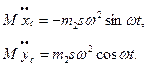(2)

Решая (1) и (2) совместно, найдем:

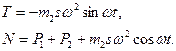
Наибольшее значение реакции 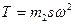. Сдвиг электродвигателя по плоскости произойдет в том случае, если силы трения плоскости окажутся меньше, чем 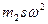. Наименьшее значение реакции 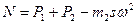. Двигатель может оторваться от плоскости и подпрыгнуть, если .

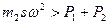Дата добавления: 2015-06-27