Центробежные моменты инерции. Понятие о главных осях инерции тела

Центробежными моментами инерции называются величины 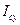, , , 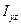определяемые равенствами , , , 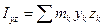где

- массы точек; 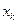, , 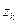- их координаты; при этом , ,

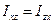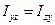
Центробежные моменты инерции могут быть как положительными, так и отрицательными величинами, и в частности при определенным образом выбранных осях могут обращаться в нули.

Рассмотрим однородное тело, имеющее ось симметрии (рис. 24)

Рис. 24

Проведем координаты оси так, чтобы ось 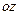была направлена вдоль оси симметрии. Тогда в силу симметрии каждой точки тела с массой и координатами 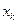, , 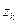будет соответствовать точка с другим индексом, но с такой же массой и с координатами равными 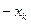, , 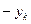. В результате получим, что и 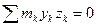. Тогда , .

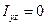Ось 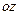, для которой центробежные моменты инерции 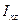, , 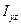содержащие в своих индексах наименование этой оси равна нулю, называется главной осью инерции тела для точки .

Из изложенного следуем, что если тело имеет ось симметрии, то эта ось является главной осью инерции тела для любой своей точки.

Главная ось инерции не обязательно является осью симметрии. Рассмотрим однородное тело, имеющее плоскость симметрии (на рис. 24 плоскостью симметрии тела является плоскость ).

Проведем в этой плоскости какие-нибудь оси 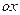, 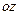и перпендикулярную им ось

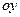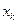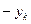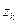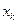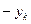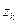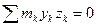. Тогда в силу симметрии каждой точке с массой и координатами, равными , , , будет соответствовать точка с такой же массой и координатами, равными , , . В результате, как и в предыдущем случае, найдем, что и или , , 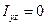откуда следует, что ось 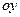является главной осью инерции для точки . Таким образом, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки , в которой ось пересекает плоскость симметрии.

Равенства , 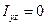выражают условия того, что ось 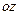является главной осью инерции тела для точки (начала координат). Аналогично, если , , 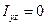то ось 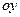будет для точки главной осью инерции. Следовательно, если все центробежные моменты инерции равны нулю, т.е , , , 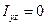то каждая из координатных осей является главной осью инерции тела для точки (начала координат).

Моменты инерции тела относительно главных осей инерции называются главными моментами инерции, построенные для центра масс тела, называют главными центральными осями инерции тела. Из доказанного выше следует, что если тело имеет ось симметрии, то эта ось является одной из главных центральных осей инерции тела, так как центр масс тела лежит на этой оси. Если же тело имеет плоскость симметрии, то ось, перпендикулярная этой плоскости и проходящая через центр масс тела, будет также одной из главных центральных осей инерции тела.

Дата добавления: 2015-06-27