Построение байесовских решающих правил

ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ РЕШАЮЩИХ ПРАВИЛ

Если оптимальные (минимаксные) решающие правила в статистической игре существуют, то они принадлежат классу байесовских решающих правил. Кроме того, байесовские стратегии находят непосредственное применение во многих статистических задачах, содержащих априорную вероятностную информацию о неизвестном состоянии природы.

Нерандомизированные байесовские решающие правила 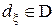составляют существенно полный подкласс в классе всех байесовских правил 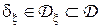относительно данного априорного распределения .

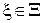Чтобы построить нерандомизированное байесовское решающее правило 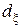относительно данного априорного распределения 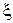, то есть обеспечить 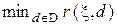, следует при каждом наблюдении случайной величины (случайного вектора) 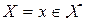выбирать решение 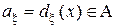, минимизирующего апостериорный условный риск

Здесь функция апостериорного распределения 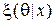характеризуется плотностью или функцией вероятностей 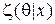, вычисляемой по формуле Байеса

, ,

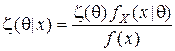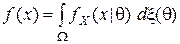где 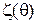, , 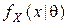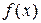- это плотности или функции вероятностей априорного распределения состояний природы 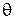, условного распределения наблюдаемой случайной величины 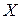при данном и маргинального (безусловного) распределения 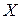, соответственно.

Заметим, что байесовский риск решающего правила 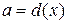и апостериорный условный риск связаны очевидным соотношением

,

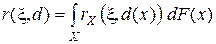где 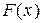- функция безусловного распределения для .

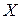Минимальный байесовский риск 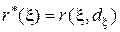является вогнутой функцией от .

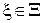Пример 1. Пусть в исходной антагонистической игре , , 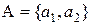а функция потерь описывается матрицей

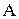Θ

:

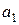
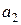
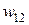
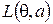Распределения вероятностей наблюдаемой случайной величины 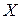характеризуются плотностями или функциями вероятностей 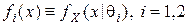. Соответствующая статистическая игра – это задача проверки простой гипотезы 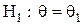против простой гипотезы 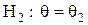при стоимости ошибок 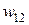, . Найдём байесовское решающее правило относительно априорного распределения 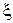, заданного априорной вероятностью 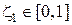состояния природы .

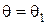По формуле Байеса

,

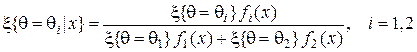то есть

, .

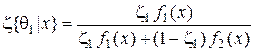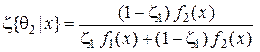Апостериорный условный риск в этой задаче равен

,

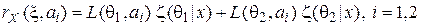или

, .

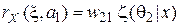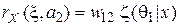При любом 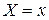следует принимать , если и в случае обратного неравенства. Таким образом, байесовское решающее правило относительно 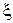при любом заданном значении 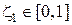имеет вид

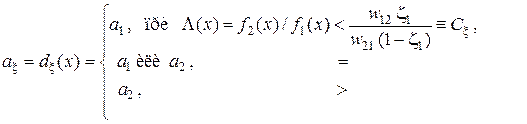
Функцию 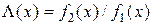называют отношением правдоподобия.

Пример 2. Пусть 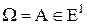и необходимо оценить неизвестный параметр семейства распределений 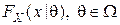, объявляя решение 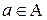при квадратичной функции потерь 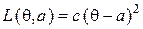, после наблюдения случайной величины 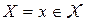. Найдём в такой задаче статистического оценивания байесовское решающее правило относительно априорного распределения 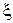, характеризуемого плотностью .

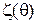При любом значении 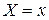имеем 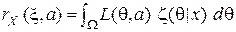, где .

В нашем примере 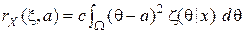. Минимизируем эту функцию, дифференцируя по 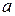и приравнивая производную нулю, что даёт

.

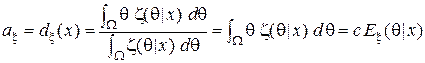Из проделанных выкладок следует, что

,

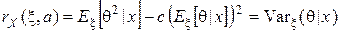а минимальный байесовский риск равен

,

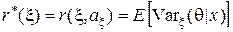где математическое ожидание берётся по безусловному распределению случайной величины .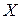

Дата добавления: 2015-06-27