Упражнения. Принцип инвариантности в статистических играх

Принцип инвариантности в статистических играх

При выборе оптимальных стратегий в статистических играх, обладающих некоторыми свойствами симметрии, то есть инвариантных относительно подходящей группы преобразований, естественно ограничиться подклассом соответственно симметричных (инвариантных) решающих правил.

Множество преобразований 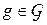, определённых на непустом пространстве 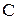, является группой. если оно замкнуто относительно композиции и обратного преобразования.

Статистическую игру называют инвариантной относительно некоторой группы преобразований 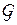над выборочным пространством , если

1. Семейство функций распределения 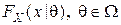, инвариантно относительно 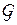, то есть для 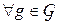и 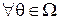существует единственный элемент 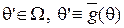такой, что 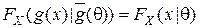; преобразования 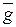над пространством 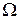составляют группу .

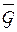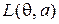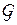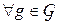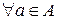2. Функция потерь инвариантна относительно , то есть для и существует единственный элемент 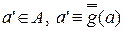такой, что 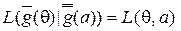; преобразования 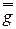над пространством составляют группу .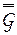

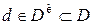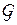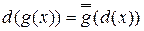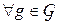В инвариантной статистической игре нерандомизированное решающее правило называется называют инвариантным относительно группы , если для и 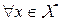. Инвариантным рандомизированным решающим правилом 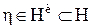называют соответствующее распределение вероятностей на 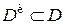. Наконец, решающее правило поведения 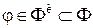, описываемое функцией распределения 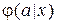на при 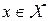, называется инвариантным относительно 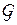, если .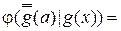

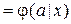Заметим, что если группа 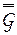преобразований над содержит только линейные преобразования вида 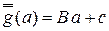, то инвариантные нерандомизированные решающие правила образуют существенно полный класс среди всех инвариантных правил.

Два состояния природы 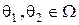называются эквивалентными, если существует такое преобразование 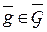, что 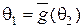. Это соотношение эквивалентности разбивает множество 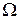на так называемые орбиты 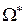. Если статистическая игра инвариантна относительно группы 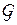, то функция риска любого инвариантного решающего правила 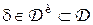постоянна на орбитах, то есть 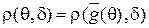для 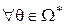, 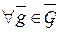. В ряде случаев и это делает инвариантные правила уравнивающими, что позволяет отыскивать инвариантное минимаксное решающее правило как наилучшее инвариантное правило, то есть такое 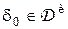, что .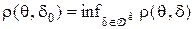

Теорема 1. Пусть статистическая игра инвариантна относительно конечной группы 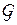. Тогда любое инвариантное минимаксное решающее правило является минимаксным.

1. Пусть случайная величина 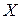имеет нормальное распределение, 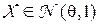, с неизвестным средним 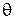и единичной дисперсие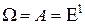й, и .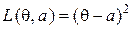

а. Покажите, что статистическая игра инвариантна относительно конечной группы переносов 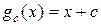. Найдите 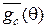и .

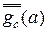б. Найдите вид инвариантных нерандомизированных решающих правил. Покажите, что они являются линейными функциями от .

2. Пусть случайная величина 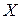имеет биномиальное распределени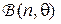е , где 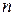известно, а 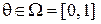. Предположим также. что 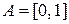и 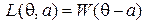есть некоторая чётная функция от .

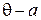а. Покажите, что статистическая игра инвариантна относительно конечной группы преобразований 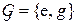, где - тождественное преобразование и 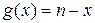. Найдите группы 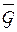и .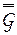

б. Найдите вид инвариантных нерандомизированных решающих правил.

3. (Фергюсон [6]). Вероятность 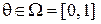успеха в единственном испытании Бернулли, 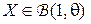, неизвестна. Пусть в этой задаче 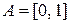, 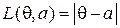. Найдите минимаксное решающее правило и значение соответствующей статистической игры, используя принцип инвариантности.

Указания. 1. Покажите, что эта статистическая игра инвариантна относительно конечной группы 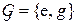, с 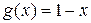; опишите группы преобразовани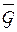й и .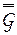

2. Покажите, что при решении этой статистической игры можно ограничиться инвариантными нерандомизированными правилами. Запишите выражение для риска 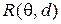, определив решающее правило 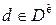в виде точки на 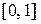; воспользуйтесь симметрией функции риска относительно .

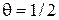3. Определите минимаксное решающее правило 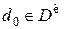в виде точки на 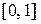, дающей 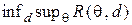, и запишите значение игры.

4. Пусть в упр. 3 функция потерь 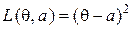(см. Пример п. 4.2). Найдите минимаксное решающее правило и значение игры, используя принцип инвариантности.

5. Пусть по одному разу подбрасываются две монеты: одна правильная (с вероятностью выпадения герба, равной 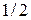), а другая гнутая (с неизвестной вероятностью 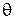выпадения герба, 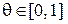). Необходимо оценить 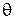, как 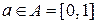, при квадратичной функции потерь 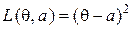, не зная, какая из монет гнутая. Найдите минимаксное решающее правило и значение игры, используя принцип инвариантности.

Утверждение Теоремы 1 справедливо и тогда, когда 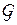есть компактная топологическая группа.

Важным случаем статистической игры, инвариантной относительно бесконечной группы преобразований, является задача оценивания параметра сдвига. Действительный параметр 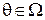называют параметром сдвига для распределения случайной величины 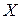, если 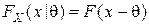, где 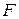есть некоторая функция распределения. В статистической игре оценивания неизвестного параметра сдвига 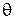предполагается, что функция потерь зависит только от 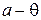, , причём , .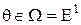

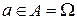Упражнение

6. а. Покажите, что статистическая игра оценивания параметра сдвига инвариантна относительно группы 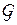переносов 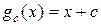. Найдите группы 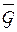и .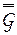

б. Покажите, что в такой игре можно исключить рандомизацию в классе инвариантных решающих правил и что инвариантные нерандомизированные правила здесь имеют вид 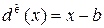, где 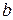- произвольное действительное число.

в. Покажите, что риск таких инвариантных правил не зависит от 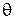, то есть .

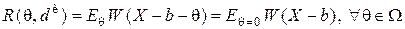Теорема 2. Наилучшее инвариантное решающее правило оценивания параметра сдвига 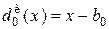, определяемое из условия

,

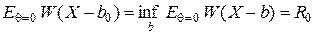является минимаксным в двух важных случаях:

а) если функция 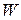ограничена;

б) если функция 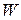непрерывна 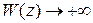и при .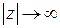

При этом значение игры равно постоянному риску .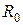

Пример. Если 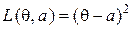и случайная величина 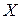имеет конечную дисперсию, то 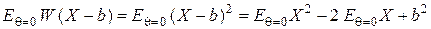. Минимизируя по 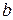, находим 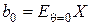, то есть 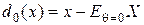. Здесь 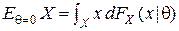. Так, в задаче оценивания неизвестного среднего 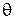для нормально распределённой случайной величины 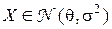, мы имеем 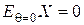и .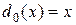

Упражнение

7. Решите задачу, поставленную в упр. 8, п. 4.2, используя принцип инвариантности.

Дата добавления: 2015-06-27