Локальная равновесность

Локальная изотропность

Основные допущения двухпараметрических МТ

Двухпараметрические МТ

Двухпараметрические модели турбулентности образуются добавлением к системе основных уравнений газовой динамики двух независимых уравнений переноса для кинетической энергии турбулентности и какого-либо другого независимого параметра (масштаба, диссипации, частоты и т.д.). Таким образом, двухпараметрические модели оказываются самодостаточными.

Однако это свойство весьма обманчиво, т.к. при их построении использовался рад допущений, в некоторых случаях двухпараметрические модели будут давать неверный результат. Поэтому необходимо очень четко представлять эти допущения.

Поскольку уравнение КЭТ было рассмотрено выше, уделим основное внимание записи второго уравнения и их взаимной увязке.

Это означает равенство пульсационных составляющих скорости u^’=v^’=w^’. Вполне корректно для мелких вихревых образований, например на высоких числах Рейнольдса, однако для крупных вихрей весьма спорно. Например, в отрывных течениях именно это допущение «ответственно» за некорректность расчетов.

Предполагается, что генерация и диссипация турбулентности локально равны. Это допущение необходимо для расчета рейнольдсовых напряжений.

Кроме того, по гипотезе Буссинеска, пульсационные составляющие потока пропорциональны осредненным локальным величинам (см. (7.30)), т.е. турбулентная вязкость может быть определена методом анализа размерностей через осредненные величины. Например, в k-e модели 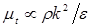, в k-w модели .

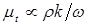Данные допущения справедливы для довольно широкого класса инженерных задач, однако неверны для отрывных течений, течений вблизи искривленных поверхностей, течений, подверженных сильным градиентам давления и т.д.

Стандартная k- e модель турбулентности

Не так давно k-e -модель являлась наиболее популярной моделью турбулентности. Первые усилия по ее разработке были предприняты Чоу (1945), Давыдовым (1961), Харлоу и Накаямой (1968). Однако центральной работой в этом направлении была статья Лаундера-Джонса (1972), получившая дальнейшее развитие и обобщение в исследованиях Лаундера-Сполдинга (1972) и Лаундера-Шармы (1974). Сформировалось понятие стандартной k-e модели, построенной в предположении о реализации полностью развитых турбулентных течений при больших турбулентных числах Рейнольдса Re→∞.

В 70—80-х годах XX в. появилось целое семейство k-e моделей (см., например, Лаундер-Приддин-Шарма (1977), Лэм-Бремхерст (1981), Чен (1982) и др.). В результате был достигнут существенный прогресс в расчетах различных типов течений, в том числе сдвиговых турбулентных. Это послужило основанием для включения моделей типа k-e во все вычислительные программы, а также в коммерческие пакеты, предназначенные для решения широкого круга задач прикладной аэродинамики и теплообмена (STAR-CD, FLUENT, PHOENICS, FIRE, FLOW3D и ряд других).

Формулу для скорости диссипации (рассеивания) энергии турбулентности можно на основании (7.29) записать в виде

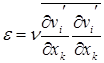. (7.32)

Суммируя уравнения для энергии турбулентных пульсаций k, скорости диссипации турбулентной энергии e, выражение для кинетической турбулентной вязкости и записывая комплект стандартных констант, представим стандартную k-e модель, записанную в тензорной форме

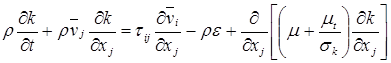
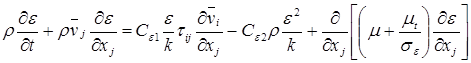(7.33)

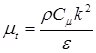
и константы замыкания (Rodi, 1980)

C_e1=1,44, C_e2=1,92, C_m=0,09, s_k=1,0, s_e=1,3. (7.34)

RNG k-e модель турбулентности

RNG k-e модель была разработана на основе строгих статистических методов (renormalization group theory). Она аналогична стандартной k-e модели, но имеет ряд существенных отличий:

Дополнительное условие в уравнении скорости турбулентной диссипации e улучшает точность решения высоконапряженных потоков.

Дополнительный параметр, учитывающий циркуляцию турбулентности, улучшает точность расчета течений с закруткой потока.

RNG теория предлагает аналитическую формулу турбулентных чисел Прандтля, в то время, как в стандартной k-e модели данный параметр является константой.

В то время, как стандартная k-e модель является высокорейнольдсовой моделью, RNG теория предоставляет полученную аналитическим путем дифференциальную формулу эффективной вязкости, что более приемлемо при расчете низкорейнольдсовых течений. Но стоит отметить, что данная формула работает при качественном сеточном разрешении в области пограничного слоя.

Эти особенности делают RNG k-e модель более точной и надежной для широкого диапазона турбулентных течений, чем в случае со стандартной k-e моделью.

RNG k-e модель показывает существенное преимущество перед стандартной k-e моделью турбулентности для искривленных, вихревых и вращающихся потоков.

Стандартная k-w модель турбулентности

Запишем уравнения еще одной популярной двухпараметрической МТ - k-w в форме данной Уилкоксом в 1988. w - может рассматриваться как обратная величина временного масштаба диссипации.

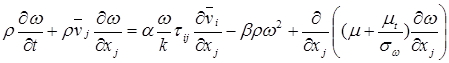(7.35)

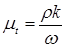
и константы замыкания

a=5/9, b=3/40, b^*=9/100, s_w=1/2, s_e=1/2. (7.36)

Модель переноса касательных напряжений SST k-w

Данная модель имеет англоязычную аббревиатуру "SST" (Shear-Stress Transport), является разновидностью стандартной k-w модели и была разработана Ментером. Данная модель эффективно сочетает устойчивость и точность стандартной k-w модели в пристеночных областях и k-e модели на удалении от стенок. SST k-w модель имеет следующие особенности по сравнению со стандартной k-w моделью:

Стандартная k-w модель и преобразованная k-e модель объединяются специальной функцией и обе добавлены в представленную модель. Специальная функция в пристеночной области принимает значение единицы, активизируя стандартную k-w модель, а на удалении от стенки принимает значение нуля, активизируя преобразованную k-e модель.

Определение турбулентной вязкости модифицировано для представления уравнения переноса касательных напряжений.

Отличаются константы моделей турбулентности.

Эти особенности делают SST k-w модель более точной и надежной для широкого класса потоков (т.е., потоков подверженных градиентам давления, обтекание профилей, околозвуковые ударные волны), чем в случае стандартной k-w модели.

Дата добавления: 2015-06-28