Уравнение кинетической энергии турбулентности

Однопараметрические МТ

Для того чтобы учесть предысторию потока создаются более сложные МТ. Первым шагом на этом пути является введение в основную систему уравнений одного дополнительного дифференциального уравнения. В нем могут рассматриваться различные характеристики турбулентности, однако наиболее популярным методом является использование масштаба характеристической турбулентной скорости как корня квадратного из удельной кинетической энергии турбулентности k.

Кинетической энергией турбулентности будем в дальнейшем называть

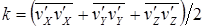(7.27)

Далее, в целях упрощения понимания физического смысла уравнений, используем индексную форму записи, в которой повторяющиеся индексы обозначают операцию суммы (например, ).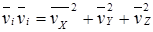

Уравнение для k можно вывести из уравнения Рейнольдсовых напряжений, помня, что k есть полусумма нормальных Рейнольдсовых напряжений

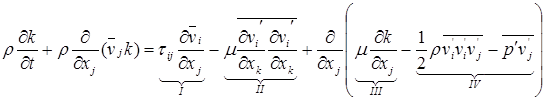. (7.28)

Рассмотрим физический смысл каждого из членов уравнения (7.28). Члены в левой части описывают нестационарный и переносный (конвективный) темп изменения кинетической энергии турбулентности (КЭТ).

Первый член в правой части уравнения (7.28) обычно называется членом генерации и отражает удельную кинетическую энергию турбулентности на единицу объема вследствие действия сил трения в потоке. Этот член описывает потери энергии для осредненного потока на подпитку турбулентных пульсаций.

Второй член в правой части уравнения (7.28) известен как диссипативный и показывает средний удельный темп распада наименьших вихрей. Этот процесс - переход кинетической энергии в тепловую на молекулярном уровне посредством трения. Диссипация обозначатся e и определяется из второго члена правой части уравнения (7.28)

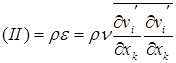. (7.29)

Отметим, что диссипация всегда положительна, т.е. в уравнении КЭТ всегда является стоком.

Третий член правой части уравнения (7.28) описывает диффузию (а не разрушение) k посредством молекулярного движения

.

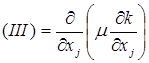Четвертый член правой части уравнения (7.28) описывает изменения k за счет сложных совместных флуктуаций скорости и давления

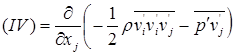
В целом все эти члены имеют смысл и форму общую для любого уравнения переноса. Отметим, что III и IV член уравнения лишь перераспределяют k в потоке. Генерация (I) и диссипация (II) являются единственными источниками и стоками k.

Однако, при моделировании возникает проблема замыкания и следовательно, чтобы проинтегрировать данное уравнение надо ввести некие корреляции для касательных напряжений, диссипации и диффузии, основанные на экспериментальном материале. В общем случае можем записать для плоского потока несжимаемой жидкости

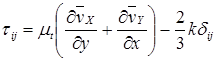, (7.30)

где m _t – есть турбулентная или «кажущаяся» вязкость, k –кинетическая энергия турбулентности, d_ij - оператор Кронекера.

Турбулентная вязкость рассматривается на аналогичной основе (как и в алгебраических МТ)

,

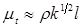где l –масштаб турбулентности (подобно записи 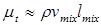для алгебраических моделей).

В данном определении в неявном виде заложено предположение о том, что турбулентность характеризуется временным масштабом, пропорциональным временному масштабу осредненного потока. Это верно не для всех потоков, и иногда приводит к неточностям в расчетах. Кроме того, еще более грубое неявно введенное приближение – это изотропность турбулентности.

Дата добавления: 2015-06-28