Пристеночные течения

Свободно-турбулентные течения

Термин «свободно-турбулентные течения» может быть рассмотрен как не ограниченный никакими твердыми поверхностями. В качестве примера можно привести три типа течения: турбулентный след за телом, слой смешения и свободная струя.

Для каждого из трех случаев вводится предположение, что длина пути смешения есть некая константа, помноженная на локальную толщину турбулентного слоя

l_mix. =ad(x).

	Тип течения	Турбулен­тный след	Плоская струя	Круглая струя	Плоский слой смешения
a	0.180	0.098	0.080	0.071

В свободно-турбулентных течениях длина пути смешения рассматривается как константа поперек слоя и изменяется пропорционально толщине турбулентного слоя. Для течения вблизи твердой поверхности следует определить способ описания, в соответствии с физической природой (см. рис. 7.6).

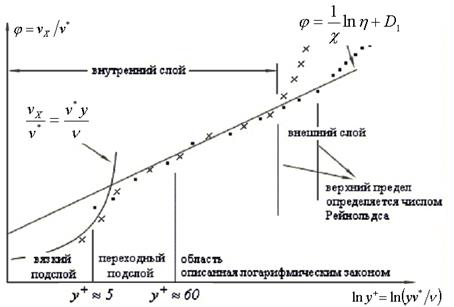
Рис.7.6 Представление пристеночной области

На основании экспериментальных фактов можно показать, что при обтекании плоской пластины количество движения меняется пренебрежимо мало, касательные напряжения практически постоянны и выполняется соотношение

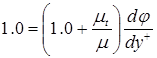
В вязком подслое, где вязкие силы подавляют турбулентные пульсации, указанное уравнение перейдет в j=y⁺ и в виде турбулентной вязкости может быть записана как

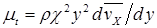(7.26)

Три наиболее известных модификации модели пути смешения реализованы в МТ Ван Дриста, Шебеки-Смита и Болдуина-Ломакса.

В целом, алгебраические модели турбулентности показывают хорошее совпадение с экспериментом для таких случаев как развитое течение в трубе или течение в безградиентном пограничном слое, поскольку их константы были настроены именно на эти случаи. Для отрывных течений алгебраические модели турбулентности оказываются несостоятельны, вследствие неспособности учесть предысторию потока.

Дата добавления: 2015-06-28