Аналитическая геометрия на плоскости. Стратегические ориентиры развития вариативного содержания образования

Стратегические ориентиры развития вариативного содержания образования

Стратегия развития вариативного образования в Украине

В Украинском государстве происходят эпохальные политические, социокультурные, духовные и экономические изменения. Они привели к тому, что общество постепенно переходит от относительно стабильной предсказуемой фазы к динамической непредсказуемой фазе развития. Больше не существует государственной единой и обязательной для всех идеологии. Каждый волен иметь любые взгляды, свободно выражать свое мнение. Возросла социальная, духовная и экономическая дифференциация общества. Индивидуальные цели жизни личности начали признаваться обществом как не менее значимые, чем коллективные и общественные цели. Все это не могло не повлиять на образовательную политику страны, на те существенные изменения, которые привносились в содержание образования в последние годы работы нашей школы.

В целях перехода от адаптивно-дисциплинарной модели унифицированного образования к личностно-ориентированной модели вариативного образования разрабатываются и внедряются в школе программы «Творческая одаренность», «Социально-психологическая поддержка, обучение и воспитание детей с аномалиями развития», «Социальная служба помощи детям и молодежи» и многие другие.

По своей направленности эти программы предназначаются для решения следующих задач:

• возрождение ориентации на индивидуальность ребенка;
• расшатывание мифа об «одинаковости» всех детей;
• формирование в обществе объективной потребности в создании психологической службы образования, нацеленной на профилактическую, диагностическую, развивающую, коррекционную и реабилитационную работу с личностью.

Стратегическими ориентирами развития вариативного содержания образования являются следующие:

1. От отдельных альтернативных научных педагогических школ, разрабатывающих проблемы школьного содержания образования, к системе вариативных инновационных технологий в контексте культурно-исторической педагогики развития. В этом контексте в развитии вариативного образования важную роль играют авторские школы, которые подразделяются на два типа — инструментальные и культурологические. В фокусе внимания инструментальных школ находится, как правило, тот или иной конкретный метод, найденный в практической деятельности благодаря таланту педагога-новатора. Иное происхождение имеют культурологические авторские школы. Они рождаются, как правило, на стыке мировоззренческих концепций с инновационными технологиями. Например, вальдорфская педагогика с ее специфическим содержанием образования исходит из философии Р. Штайнера. Особо следует обратить внимание на такие культурологические авторские школы, как дидактическая система обучения Л.В. Занкова, система развивающего обучения Эльконина-Давыдова, школа диалога культур Библера.
2. От монополии государственного образования к сосуществованию и сотрудничеству государственного, негосударственного и семейного воспитания со спецификой содержания, свойственной каждому из этих видов, но с учетом государственных стандартов образования.
3. От унитарной школы, работающей по единым нормативным документам, к дифференциации содержания образования в системе общего образовательного пространства России. Реальные возможности приобщения детей различных этносов к культуре открывает «Базисный учебный план общеобразовательных учреждений Российской Федерации», в котором федеральный компонент образования сочетается с регионально-национальным и школьным. Ярким примером системной культурологической программы является программа курса М.Ю. Новицкой «Введение в народоведение» для начальной школы.
4. От предметоцентризма к культурологической концепции содержания образования, преодолевающей узкий «знаньевый» подход к его формированию. Выделение ключевых компетенций в конкретном содержании и образовательных областей в учебном плане — проявление той же тенденции.
5. От «чистых» линий развития типов общеобразовательных учреждений к «смешанным» линиям развития видов общеобразовательных учреждений. Показателем тому является опыт слияния школы с детским садом, школы с вузом. В Москве и других городах появились «школы-гибриды» с научно-исследовательскими институтами — «школы-лаборатории», «научно-учебные методические комплексы» и др.
6. Школа успешно продвигается по пути от монопольного учебника к вариативным учебникам, а также от монофункциональных технических средств обучения к полифункциональным средствам и информационным технологиям. Происходит постепенное изменение технических средств обучения по их функции и месту в учебном процессе, характеризующееся переходом от наглядно-демонстрационных к обучающим (ЭВМ), от отдельных приборов и пособий к микролабораториям. Таковы те изменения в содержании школьного образования, которые характерны для эпохи коренного преобразования российской школы.

Вопросы и задания для самоконтроля

1. Выпишите из текста главы основные понятия, принципы и факторы отбора содержания образования.
2. Постройте из них логическую схему, которую начните так:

ОБРАЗОВАНИЕ

СОДЕРЖАНИЕ ОБРАЗОВАНИЯ

принципы отбора содержания

факторы отбора содержания

носители содержания

учебный план.

1. Раскройте содержание общих принципов формирования содержания общего среднего образования.
2. Обсудите с коллегами проблему дифференцированного содержания образования.
3. Представьте, что вы с коллегами создаете школу и разрабатываете учебный план... Какой он будет? Сделайте его проект.
4. Стандартизация выпуска продукции является общепризнанной во всем мире. Применима ли стандартизация в сфере образования? Обоснуйте свой ответ.

Рекомендуемая литература для самостоятельной работы по предмету «Процесс обучения как целостная система»

Амонашвили Ш.А. Обучение. Оценка. Отметка. М., 1980.

Анисимов Н. Слагаемые инновационного потенциала // Директор школы. — 1993.

Беспалъко В.П. Слагаемые педагогической технологии. М., 1989.

Бондаренко СМ. Учить детей сравнивать. М., 1981.

Бургин М.С. Инновации и новизна в педагогике // Педагогика. — М., 1998, № 12.

Выбор методов обучения в средней школе / Под ред. Ю.К. Бабанского. М., 1981.

Выготский Л.С. Собр. Соч. Т. 6. М., 1984.

Габай Т.В. Учебная деятельность и ее средства. М., 1988.

Тесен СИ. Основы педагогики. Введение в прикладную философию. М., 1995.

Давыдов В.В. Проблемы развивающего обучения. М., 1986.

Дидактика средней школы / Под ред. М.Н. Скаткина. М., 1982.

Дьяченко В. К. Организационная структура учебного процесса и его развитие. М., 1989.

Есипов Б.П. Основы дидактики. М., 1967.

Есипов Б.П. Самостоятельная работа учащихся на уроке. М., 1961.

Загвязинский В.И. Теория обучения. Современная интерпретация. М., 2001.

Занков Л.В. Обучение и развитие (Избр. психолог. труды). М., 1990. Часть 1, гл. 3.

Занков Л.В. Дидактика и жизнь. Избр. труды. М., 1990.

Зотов Ю.Б. Организация современного урока / Под ред. П.И. Пидкасистого. М., 1984.

Зуев Д.Д. Школьный учебник. М., 1983.

Ильина ТА. Педагогика. М., 1984.

Инновационные учебные заведения в России: Информ. справ. пособие в помощь руководителя школ. М., 1992.

Кириллова Г.Ф. Теория и практика урока в условиях развивающего обучения. М., 1980.

Коллективная учебно-воспитательная деятельность школьников / Под ред. И. Б. Первина. М., 1985.

Леднев В. С. Содержание образования. М., 1989.

Лернер И.Я. Процесс обучения и его закономерности. М., 1980.

Лернер И.Я. Проблемное обучение. М., 1974.

Лернер И.Я. Качество знаний учащихся. Какими они должны быть? М., 1978.

Лернер И.Я. Дидактические основы методов обучения. М., 1981.

Лийметс Х.И. Групповая работа на уроке. М., 1975.

Лихачев Б.Т. Педагогика. М., 1996.

Лихачев Б.Т. Воспитательные аспекты обучения. М., 1979, 1982.

Калмыкова З.И. Психологические принципы развивающего обучения. М., 1979.

Качество знаний учащихся и пути его совершенствования / Под ред. М.Н. Скаткина и В.В. Краевского. М., 1978.

Коротяев Б.И. Обучение — процесс творческий: из опыта работы. М., 1980.

Куписевич Ч. Основы общей дидактики. М., 1986.

Махмутов М.И. Организация проблемного обучения в школе. М., 1977.

Махмутов М.И. Современный урок. 2-е изд. М., 1985.

Матюшкин A.M. Проблемные ситуации в мышлении и обучении. М., 1972.

Менчинская Н.А. Проблемы учения и умственного развития школьника. М., 1989.

Наин А.Я. Педагогические инновации и научный эксперимент // Педагогика, 1996. № 5.

Педагогика / Под ред. Ю.К. Бабанского. М., 1988.

Перовский Е.И. проверка и оценка знаний в средней школе. М., 1968.

Пидкаситый П.И. Самостоятельная познавательная деятельность школьников в обучении. М., 1980.

Пидкасистый П.И., Горячев Б.В. Процесс обучения в условиях демократизации и гуманизации школы: учебное пособие. М., 1991.

Пидкасистый П.И., Коротяев Б.И. Организация деятельности учеников на уроке. М., 1985.

Подымов Л.С. Подготовка учителя к инновационной деятельности. М., 1995.

Поляков С.Ф. В поисках педагогической инноватики. М., 1989

Полонский В.М. Оценка знаний школьников. М., 1981.

Поташник М.М. В поисках оптимального варианта. М., 1984.

Поташник М.М. Инновационные школы России: становлений и развитие. М., 1996.

Сарапулов В.А. Инновации и опытно-экспериментальная работа в образовательных учреждениях: опыт педагогического осмысления проблемы. Чита, 1997.

Скаткин М.Н. Проблемы современной дидактики. М., 1970; изд. 2-е. М., 1984.

Сластенин В.А., Подымова Л.С. Педагогика: инновационная деятельность. М., 1997.

Талызина Н.Ф. Управление процессом усвоения знаний. М., 1984.

Теоретические основы процесса обучения в советской школе / Под ред. В.В. Краевского, И.Я. Лернера. М., 1989.

Харламов И.Ф. Педагогика. 2-е изд. М., 1990.

Чередов И.М. Система форм организации обучения в советской общеобразовательной школе. М., 1987.

Шамова Т.И. Активизация учения школьников. М., 1982.

Шаталов В. Ф. Куда и как исчезли тройки. М., 1979.

Шахмаев Н.М. Дидактические проблемы применения технических средств обучения в средней школе. М., 1983.

Щукина Г.И. Активизация познавательной деятельности учащихся. М., 1979.

Щукина Г.И. Проблема познавательного интереса в педагогике. М., 1971.

Юсуфбекова Н.Р. Общие основы педагогических инноваций: опыт разработки теории инновационного процесса в образовании. М., 1991.

Якиманская И. С. Технология личностно-ориентированного образования. М., 2000.

Якиманская И.С. Личностно-ориентированное обучение в современной школе. Изд. Второе. М., 2000.

Яковлев Н.М., Сохолр A.M. Методика и техника урока в школе. М., 1985.

Лекция № 1 «СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ»

1. Основные понятия

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат.

Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О — началом координат. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу) (рис. 23).

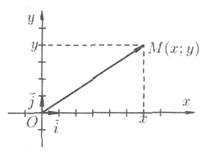
Рис. 23

На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат — вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).

Единичные векторы осей обозначают 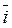и 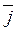(| | 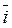=| | = 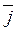1, 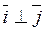). Систему координат обозначают Оху (или O ), а плоскость, в которой расположена система координат, называют координатной плоскостью.

Рассмотрим произвольную точку М плоскости Оху. Вектор 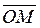на­зывается радиусом-вектором точки М.

Координатами точки М в системе координат Оху (O ) называ­ются координаты радиуса-вектора 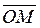. Если 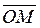= (х;у), то координаты точки М записывают так: М(х;у), число х называется абсциссой точки М, у — ординатой точки М.

Эти два числа х и у полностью определяют положение точки на плос­кости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.

Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором того же направления, что и луч Ор.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведет­ся в направлении, противоположном движению часовой стрелки) (см. рис. 24).

Числа r и φ называются полярными координатами точки М, пишут M(r;φ), при этом r называют полярным радиусом, φ — полярным углом.

Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (-π;π) (или 0 ≤ φ < 2π], а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.

Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть х и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.

Из рисунка 25 видно, что прямоугольные координа­ты точки М выражаются через полярные координаты точки следующим образом:

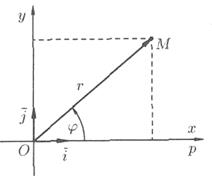
Рис. 25.

Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами:

Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что — π < φ ≤ π.

Пример 9.1. Дана точка М(-1;- ). Найти полярные координаты точки М.

Решение: Находим r и φ:

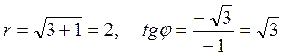
Отсюда . Но так как точка М лежит в 3-й четверти, то n = -1 и 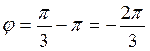. Итак, полярные координаты точки М есть r =2, φ = , т.е. М (2; ).

2. Основные приложения метода координат на плоскости

Дата добавления: 2015-06-28