Параллельный перенос осей координат

Площадь треугольника

Требуется найти площадь треугольника ABC с вершинами A(x₁;y₁), В(х₂;у₂), С(х₃; у₃).

Решение: Опустим из вершин А, В, С перпендикуляры АА₁, ВВ₁, СС₁ на ось Ох (см. рис. 27). Очевидно, что

S_ABC = S_AA1B1B + S_B1BCC1 – S_A1ACC1

Поэтому

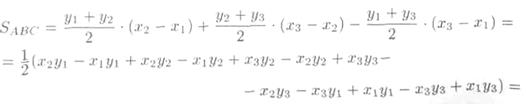
Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.

3. Преобразование системы координат

Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.

Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.

Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от систе­мы координат Оху к новой системе O₁x₁y₁, при котором меняется поло­жение начала координат, а направление осей и масштаб остаются неизменными.

Пусть начало новой системы координат точка O₁ имеет координаты (х_о;у_о) в старой системе координат Оху, т. е. O₁(x₀;y₀). Обозначим координаты произвольной точки М плоскости в системе Оху через (х;у), а в новой системе O₁x₁y₁ через (х';у') (см. рис. 28).

Рис. 28.

Рассмотрим векторы

Следовательно,

Полученные формулы позволяют находить старые координаты х и у по известным новым х' и у' и наоборот.

Дата добавления: 2015-06-28