Контрольная работа 1 страница

Поверхности второго порядка

6.1. Координаты центра эллипсоида равны …

6.2. Даны уравнения поверхностей второго порядка:
А)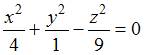
B)
C)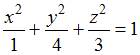
D)
Тогда однополостный гиперболоид задается уравнением …

6.3. Вершина конуса 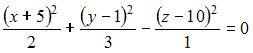имеет координаты …

6.4. Уравнение в пространстве определяет …

			параболоид
			эллипсоид
			однополостный гиперболоид
			цилиндр

«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

Контрольные варианты к задаче 1

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	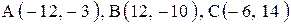.	2.	.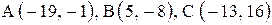
3.	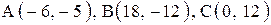.	4.	.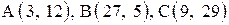
5.	.	6.	.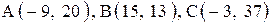
7.	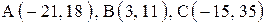.	8.	.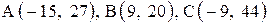
9.	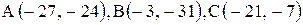.	10.	.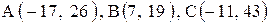
11.	.	12.	.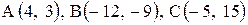
13.	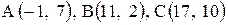.	14.	.
15.	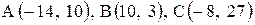.	16.	.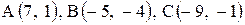
17.	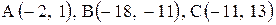.	18.	.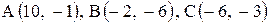
19.	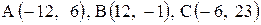.	20.	.
21.	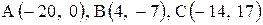.	22.	.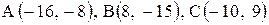
23.	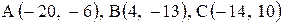.	24.	.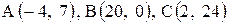
25.	.	26.	.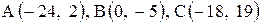
27.	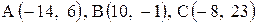.	28.	.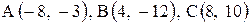
29.	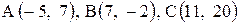.	30.	.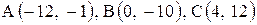

Контрольные варианты к задаче 2

1. Вершина квадрата 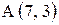, сторона СD лежит на прямой, отсекающей на осях координат отрезки 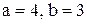. Написать уравнение стороны АД (Квадрат АВСD).

2. В треугольнике АВС даны уравнения: высоты ,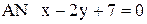

высоты 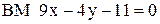и стороны 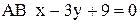. Составить уравнение третьей высоты.

3. Найти точку, симметричную точке 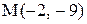относительно прямой .

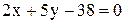4. Составить уравнение прямой, проходящей через точку пересечения прямых

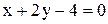и 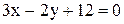и образующей угол в с прямой .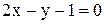

5. Через точку пересечения прямых 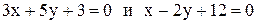провести прямую перпендикулярно прямой .

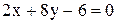6. В треугольнике АВС даны уравнения: стороны АВ и высот 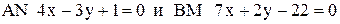. Составить уравнения двух других сторон треугольника.

7. Вычислить координаты вершин ромба, если известны уравнения двух его сторон (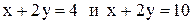) и уравнение одной из его диагоналей .

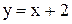8. Из точки 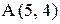выходит луч света под углом 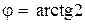к оси Ох и от нее отражается. Написать уравнения падающего и отраженного лучей.

9. Под каким углом к оси Ох наклонена прямая, проходящая через точки .

10. В квадрате АВСD даны вершина и точка - точка пересечения диагоналей. Найти уравнения сторон квадрата, не проходящих через верши-

ну А.

11. Даны точки 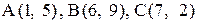. Отрезок АС разделен точкой D в отношении 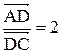. Найти расстояние от точки А до прямой ВD.

12. Отрезок прямой , заключенный между осями координат, является диагональю квадрата. Найти уравнение одной (любой) стороны квадрата.

13. Через точку пересечения прямых 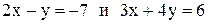провести прямую перпендикулярно прямой .

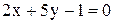14. Даны уравнения двух сторон параллелограмма: и точка пересечения диагоналей 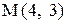. Составить уравнения двух других сторон

параллелограмма.

15. Составить уравнения прямых, проходящих через точку и составляющих угол с прямой .

16. Даны уравнения двух сторон параллелограмма 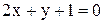- и точка пересечения его диагоналей . Составить уравнения

двух других его сторон.

17. Даны середины противоположных сторон квадрата . Написать уравнения двух сторон квадрата, на которых лежат точки .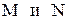

18. Провести прямую так, чтобы точка была серединой ее отрезка, заключенного между осями координат. Составить уравнение этой прямой.

19. Даны две точки: . Через середину отрезка АВ провести прямую, отсекающую от оси Ох отрезок, вдвое больший, чем отрезок на оси Оу.

20. В треугольнике АВС даны вершины: 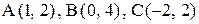. Определить: а) угол между стороной АВ и медианой стороны ВС; б) длину высоты, опущенной из вершины С.

21. Составить уравнения катетов прямоугольного равнобедренного треугольни-

ка, зная уравнение гипотенузы и вершину прямого угла .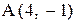

22. Составить уравнение прямой, проходящей через точку 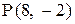и отсекающей от координатного угла треугольник площадью 8 дм².

23. В треугольнике АВС даны вершины: 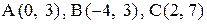. Найти точку, симметричную точке В относительно стороны АС.

24. В треугольнике АВС даны вершины: . Найти угол между медианой АМ и высотой ВН.

25. Даны точки 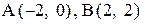. На отрезке ОА (О – начало координат), построить параллелограмм ОАСД, диагонали которого пересекаются в точке В. Написать уравнения сторон и диагоналей параллелограмма.

26. Под каким углом к оси Ох наклонена прямая, проходящая через точки ?

27.Составить уравнение прямой, проходящей через точку пересечения прямых 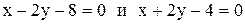и образующую с осью Ох угол, вдвое больший угла, образованного с той же осью прямой .

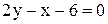28. Найти точку, симметричную точке 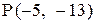относительно прямой .

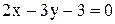29. Прямая отсекает на осях координат отрезки . Найти точку, симметричную точке 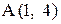относительно прямой .

30. Даны уравнения двух сторон параллелограмма: 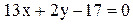- и одна из его вершин . Найти точку пересечения его диагоналей.

Контрольные варианты к задаче 3

1. Написать уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Ох параболой .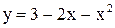

2. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 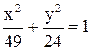, при условии, что эксцентриситет ее равен 5/4.

3. Найти точки пересечения асимптот гиперболы с окружностью,

имеющей центр в правом фокусе гиперболы и проходящей через начало координат

4. Найти длину и уравнение перпендикуляра, опущенного из фокуса параболы на прямую, отсекающую на осях координат отрезки .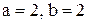

5. Составить уравнение множества точек, равноудаленных от точки 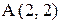и оси абсцисс. Построить чертеж.

6. Дан эллипс . Составить уравнение гиперболы, имеющей фокусы,

общие с фокусами эллипса, если известно, что эксцентриситет гиперболы равен .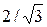

7. Составить уравнение окружности, проходящей через фокусы эллипса 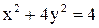и имеющей центр в его «верхней» вершине.

8. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Ох параболой .

9. Построить эллипс 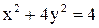и параболу 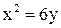и найти площадь трапеции, основаниями которой служат большая ось эллипса и общая хорда эллипса и параболы.

10. Написать уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 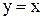и окружности 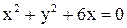и симметрична относительно оси Ох.

11. Дан эллипс 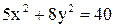. Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы - в вершинах данного эллипса.

12. Составить уравнение окружности, имеющей центр в фокусе параболы 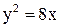и касающейся ее директрисы. Найти точки пересечения параболы и окружности.

13. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый параболой на оси Оу.

14. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Оу параболой .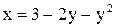

15. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом

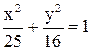, при условии, что эксцентриситет её равен 5/4.

16. Фокус параболы совпадает с центром окружности , а вершина параболы лежит в начале координат. Составить уравнение параболы и ее директрисы.

17. Написать уравнение окружности, проходящей через фокусы эллипса 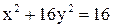и имеющей центр в его «нижней» вершине.

18. Дан эллипс 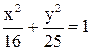. Составить уравнение гиперболы, если ее фокусы совпадают с вершинами эллипса, а ее вершины – с фокусами эллипса.

19. Составить уравнение параболы с вершиной в начале координат, если ее директриса параллельна оси Ох и проходит через «верхний» конец малой оси эллипса .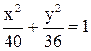

20. На параболе 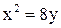найти точку, расстояние которой до фокуса равно четырем.

21. На параболе 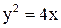найти точку, расстояние которой до фокуса равно

пяти.

22. Вершина параболы лежит в начале координат, директриса ее проходит через «правый» фокус эллипса 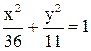. Составить уравнение параболы.

23. На прямой 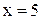найти точку, одинаково удаленную от «левого» фокуса и «верхней» вершины эллипса .

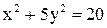24. Дано уравнение гиперболы 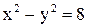. Составить уравнение эллипса, имеющего с гиперболой общие фокусы и проходящего через точку .

25. Составить уравнение окружности, диаметром которой служит отрезок пря-

мой , заключенный между осями координат.

26. Через вершину параболы 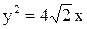проведена прямая под углом к оси Ох. Вычислить длину хорды, отсекаемой параболой на этой прямой.

27. Эллипс, симметричный относительно осей координат, проходит через точку и имеет эксцентриситет . Написать простейшие уравнение эллипса и найти расстояния от точки М до фокусов.

28. Даны вершины треугольника АСВ: 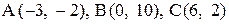. Составить уравнение окружности, для которой медиана АЕ служит диаметром.

29. Найти эксцентриситет и уравнение асимптот гиперболы, фокусы которой находятся в вершинах эллипса 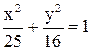, если произведение эксцентриситетов гиперболы и эллипса равно единице.

30. Составить каноническое уравнение эллипса, проходящего через точки . Найти фокусы и точки пересечения эллипса и окружности, центр которой находится в начале координат и радиус равен .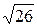

Контрольные варианты к задаче 4

Дано уравнение линии 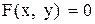. Построить линию, записав это уравнение в нормальной форме. Записать координаты фокусов. Если эта линия окажется пара-

болой, то записать уравнение директрисы.

1. 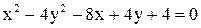.	2. .
3. 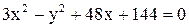.	4. .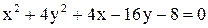
5. 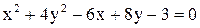.	6. .
7. 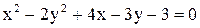.	8.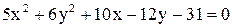
9. 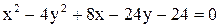.	10. .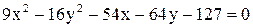
11. 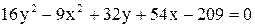.	12. .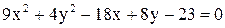
13. 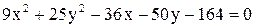.	14. .
15. .	16. .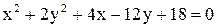
17. 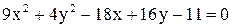.	18. .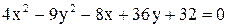
19. .	20. .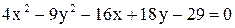
21. 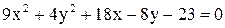.	22. .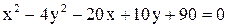
23. .	24. .
25. 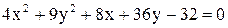.	26. .
27. .	28. .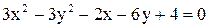
29. 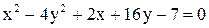.	30. .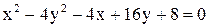

Контрольные варианты к задаче 5

Найти расстояние от точки 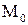до плоскости, проходящей через три точки

:

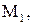
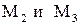1.			.
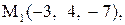
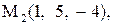
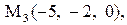
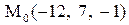2.			.
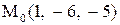3.			.
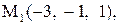
4.			.
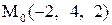5.			.
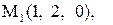
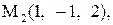
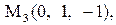
6.			.
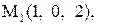
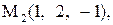
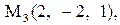
7.			.
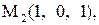
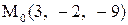8.			.
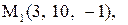
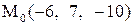9.			.
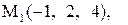
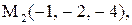
10.			.
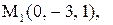
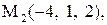
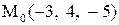11.			.
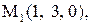
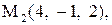
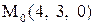12.
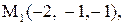
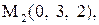
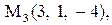
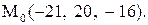
13.			.
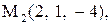
14.			.
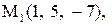
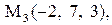
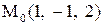15.			.
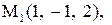
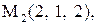
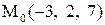16.			.
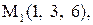
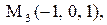
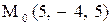17.			.
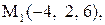
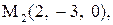
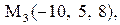
18.			.
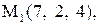
19.			.
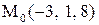20.			.
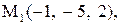
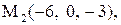
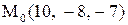21.			.
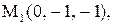
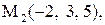
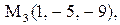
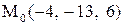22.			.
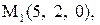
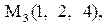
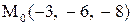23.			.
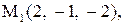
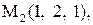
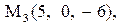
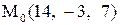24.			.
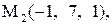
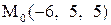25.			.
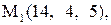
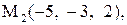
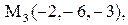
26.			.
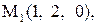
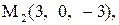
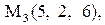
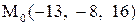27.			.
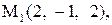
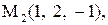
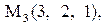
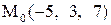28.			.
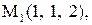
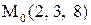29.			.
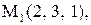
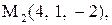
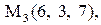
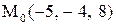30.			.

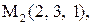
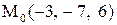Дата добавления: 2015-06-28