Построение проверяющего теста. Рисунок 2. 2 — функциональная схема объекта диагноза

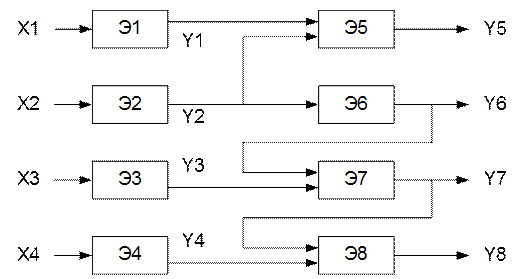
Рисунок 2.2 — Функциональная схема объекта диагноза

Функциональная схема объекта диагноза (рис. 2.2) содержит восемь элементов — Э1 - Э8, имеет четыре внешних входных воздействия — Х1 - Х4 и формирует четыре выходные реакции — У5 - У8. Каждый элемент формирует свою выходную реакцию Y, причем выходные реакции элементов Э5 - Э8 совпадают с выходными реакциями схемы. Примем, что X_i=1 и Y_j=1, если i-е входное воздействие или выходная реакция j-го элемента являются допустимыми; в противном случае X_i=0 и Y_j = 0. Состояние системы, содержащей n элементов, обозначают n-разрядным двоичным числом, в котором i-й разряд равен 1 (0), если i-й элемент исправен (неисправен). В общем случае система из n элементов имеет 2ⁿ состояний, из которых одно исправное и 2^n-1 неисправных. Ограничимся рассмотрением только одиночных неисправностей, поэтому система имеет восемь состояний:

S₀= 11111111

S₁= 01111111

S₂= 10111111

S₃= 11011111

S₄= 11101111

S₅= 11110111

S₆= 11111011

S₇= 11111101

S₈= 11111110

Каждая проверка имеет 2^k исходов, где k — число контролируемых элементов. Общее число проверок 2ⁿ, где n-число элементов системы. На практике большое число проверок не может быть осуществлено, так как нет доступа к выходам некоторых элементов; невозможно подключиться сразу к выходам нескольких элементов и т. п.

В рассматриваемом случае будем считать, что возможны только те проверки, которые заключаются в измерении реакции на выходе одного из элементов системы, причем для измерения доступны выходы всех элементов. Обозначим элементарную проверку как π_i — это контроль реакции на выходе i-го элемента (i=1, 2, …, 8).

Таблица 2.2 представляет собой ТФН, составленную для заданной системы (см. рис. 2.2).

Таблица 2.2 — Таблица функций неисправностей

Проверка	Результат R проверки для системы, находящейся в состоянии:
S0	S1	S2	S3	S4	S5	S6	S7	S8
π1
π2
π3
π4
π5
π6
π7
π8

Когда сиcтема исправна (состояние S₀), на выходах всех элементов имеют место допустимые значения сигналов. Отказ какого-либо элемента вызывает появление недопустимого значения сигнала на его выходе и на выходах всех связанных с ним элементов.

Данная ТФН содержит всю необходимую информацию для построения проверяющего и диагностического тестов. Каждая графа ТФН задает некоторую функцию, определяемую на множестве проверок. Функция равна единице, если проверка дает допустимый результат. Обозначим F — функция исправного объекта; f_i — функция i-го состояния неисправного объекта или функция i-й неисправности. Имеем:

F=π₁v π₂v π₃v π₄v π₅v π₆v π₇v π₈

f₁= π₂v π₃v π₄v π₆v π₇v π₈

f₂= π₁v π₃v π₄

f₃= π₁v π₂v π₄v π₅v π₆

f₄= π₁v π₂v π₃v π₅v π₆v π₇

f₅= π₁v π₂v π₃v π₄v π₆v π₇v π₈

f₆= π₁v π₂v π₃v π₄v π₅

f₇= π₁v π₂v π₃v π₄v π₅v π₆

f₈= π₁v π₂v π₃v π₄v π₅v π₆v π₇

При построении проверяющего теста Т_п для каждой неисправности вычисляют проверяющую функцию:

φ_i=F○f_i (2.1)

Функция φ_i=1 только на тех проверках, на которых результаты проверок различны для исправной схемы и для схемы с i-й не исправностью. Иначе говоря, она объединяет те проверки, на которых i-я неисправность обнаруживается.

φ₁= π₁v π₅

φ₂= π₂v π₅v π₆v π₇v π₈

φ₃= π₃v π₇v π₈

φ₄= π₄v π₈

φ₅= π₅

φ₆= π₆v π₇v π₈

φ₇= π₇v π₈

φ₈= π₈

Проверяющий тест:

Т_п= φ₁∙ φ₂∙…∙ φ_i∙…∙ φ_n (2.2)

где n — число неисправностей.

Т_п= φ₁∙ φ₂∙ φ₃∙ φ₄∙ φ₅∙ φ₆∙ φ₇∙ φ₈=

=(π₁v π₅)∙(π₂v π₅v π₆v π₇v π₈)∙(π₃v π₇v π₈)∙(π₄v π₈)∙

∙ π₅∙(π₆v π₇v π₈)∙(π₇v π₈)∙ π₈ (2.3)

Выражение 2.3 может быть упрощено на основе закона поглощения:

a∙(avb)=a∙ava∙b=ava∙b=a∙(1vb)=a (2.4)

Таким образом, получим:

Т_п=(π₂v π₅v π₆v π₇v π₈)∙ π₅∙ π₈= π₅∙ π₈ (2.5)

Из уравнения 2.5 следует, что для полной проверки системы необходимо и достаточно подать на внешние входы допустимые воздействия и измерить реакции на выходах двух элементов - Э5 и Э8. Если система исправна, то на выходах этих элементов будут допустимые сигналы, если же неисправна, то на выходе хотя бы одного элемента будет недопустимый сигнал.

В общем случае для проверки исправности или работоспособности объекта достаточно проконтролировать все его внешние выходы. Однако логическая модель и ТФН позволяют найти такую минимальную совокупность проверок, в которую не войдут внешние выходы объекта, являющиеся также входами блоков модели.

Дата добавления: 2015-06-28