Метод цепей и сечений

ПОСТРОЕНИЕ ДИАГНОСТИЧЕСКОГО ТЕСТА

Для построения диагностического теста, согласно выражению 2.6, для каждой пары неисправностей ТФН находим различающую функцию:

φ_1,2=1v3v5v7

φ_1,3=0v1v3v4

φ_1,4=1v2v3v6

φ_1,5=1v3v6

φ_1,6=1v3v5v7

φ_1,7=0v1v3v4

φ_1,8=3

φ_2,3=0v4v5v7

φ_2,4=2v5v6v7

φ_2,5=5v6v7

φ_2,6= —

φ_2,7=0v4v5v7

φ_2,8=1v5v7

φ_3,4=0v2v4v6

φ_3,5=0v4v6

φ_3,6=0v4v5v7

φ_3,7= —

φ_3,8=0v1v4

φ_4,5=2

φ_4,6=2v5v6v7

φ_4,7=0v2v4v6

φ_4,8=1v2v6

φ_5,6=5v6v7

φ_5,7=0v4v6

φ_5,8=1v6

φ_6,7=0v4v5v7

φ_6,8=1v5v7

φ_7,8=0v1v4

Диагностический тест первого вида определяем согласно выражению 2.7, при этом предполагается, что диагностируемая схема неисправна.

Диагностический тест имеет вид:

Т_д= φ_1,2∙ φ_1,3∙ φ_1,4∙ …∙ φ_4,8∙ …∙ φ_7,8=

=(1v3v5v7)∙(0v1v3v4)∙(1v2v3v6)∙(1v3v6)∙3∙(0v4v5v7)∙(2v5v6v7)∙

∙(5v6v7)∙(0v2v4v6)∙(0v4v6)∙(0v1v4)∙2∙(1v2v6)∙(1v6)=

=2∙3∙(0v4v5v7)∙(5v6v7)∙(0v4v6)∙(0v1v4)∙(1v6) (2.16)

После выполнения процедуры минимизации полученного выражения и рассмотрения всего множества диагностических тестов получим, что оно содержит два минимальных теста:

Т_д1=0∙2∙3∙6

Т_д2=2∙3∙4∙6

Словарь неисправностей для Т_д1 представлен в таблице 2.7.

Словарь неисправностей для Т_д2 представлен в таблице 2.8.

Таблица 2.7 — Словарь неисправностей для Т _{д 1}

Входной набор

F

f1

f2

f3

f4

f5

f6

f7

f8

при внесении неисправности

№

a

b

c

a^1

a^0

b^1

b^0

c1^1

c1^0

c2^1

c2^0

Таблица 2.8 — Словарь неисправностей для Т _{д 2}

Входной набор

F

f1

f2

f3

f4

f5

f6

f7

f8

при внесении неисправности

№

a

b

c

a^1

a^0

b^1

b^0

c1^1

c1^0

c2^1

c2^0

Поиск неисправности в заданной схеме осуществляется следующим образом. На входы схемы последовательно подают входные наборы, входящие в диагностический тест. Для каждого случая фиксируют значения выхода схемы по состоянию реле F. Полученные результаты сравнивают с данными, приведенными в словаре неисправностей. Совпадение состояний выхода и состояний, приведенных в словаре неисправностей, указывает на неисправность или на класс эквивалентных неисправностей.

Точное указание неисправности внутри класса эквивалентных неисправностей возможно только при измерениях во внутренних точках схемы, соответствующих классу эквивалентных неисправностей.

Диагностический тест второго вида определяется в том случае, если заранее неизвестно, что тестируемая схема неисправна. В этом случае диагностический тест Т_д′ определяется по выражению 2.12.

Т_д′=Т_п∙ φ_1,2∙ φ_1,3∙ φ_1,4∙ …∙ φ_4,8∙ …∙ φ_7,8=

=0∙1∙5∙6∙2∙3∙(0v4v5v7)∙(5v6v7)∙(0v4v6)∙(0v1v4)∙(1v6) (2.17)

После минимизации полученного выражения получаем множество диагностических тестов. Из результатов анализа полученного множества следует, что оно содержит один минимальный тест Т_д′=0∙1∙2∙3∙5∙6

Словарь неисправностей для минимального диагностического теста Т_д′ представлен в таблице 2.9.

Таблица 2.9 — Словарь неисправностей для Т _д ′

Входной набор

F

f1

f2

f3

f4

f5

f6

f7

f8

при внесении неисправности

№

a

b

c

a^1

a^0

b^1

b^0

c1^1

c1^0

c2^1

c2^0

Поиск неисправности в схеме осуществляется также, как и в случае диагностического теста Т_д.

При расчете тестов на ЭВМ для хранения ТФН из-за ее большого размера требуется большой объем памяти, что снижает размерность решаемых задач. В связи с этим для различных объектов диагноза разработаны специальные модели методы, которые не имеют универсального характера, но с учетом особенностей объекта позволяют более просто решать задачи построения тестов.

Так для релейно-контактных схем при построении проверяющих тестов используют метод цепей и сечений.

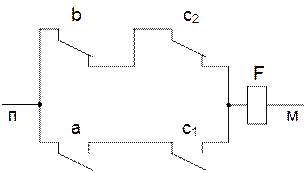
Рисунок 2.5 — Релейно-контактная схема

Под цепью понимается набор состояний контактов, которые обеспечивают наличие цепи проводимости между полюсами схемы.

Под сечением понимается набор состояний контактов, которые обеспечивают разрыв всех цепей схемы.

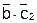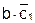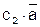Рассматриваемая схема (см. рисунок 2.5) имеет две цепи: G₁= и G₂=a∙c₁, а также содержит три сечения: H₁= , H₂= и Н₃= 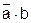. Все остальные цепи и сечения содержат противоречия, поэтому из рассмотрения исключаются.

Перечисление всех цепей и сечений однозначно задает схему.

Под цепью, урезанной на каком-либо контакте, понимается набор состояний контактов, соответствующий данной цепи, из которого иск­лючен этот контакт. Аналогично определяется сече­ние, урезанное на каком-то контакте.

Для того чтобы проверить некоторый кон­тактана отсутствие неисправности типа «разрыв», необходимо обес­печить наличие какой-либо цепи, содержащей этот контакт, и обрыв всех других цепей, в которые не входит данный контакт. Тогда при отсутствии неисправности схема будет замкнута, а о наличии неисп­равности будет свидетельствовать разомкнутое состояние схемы.

При проверке некоторого контакта на отсутствие неисправности типа «короткое замыкание» необходимо обеспечить разрыв всех цепей схемы и наличие хотя бы одной цепи, разорванной только на данном контакте. Тогда при отсутствии неисправности схема будет разомкну­та, а о наличии неисправности будет свидетельствовать замкнутое состояние схемы.

В алгоритм вычисления проверяющей функции контакта для неисправности типа «разрыв» (φ⁰) выписывают все цепи, содержащие этот контакт, определяют все сечения, содержащие этот контакт,определя­ют все сечения, урезанные на контакте «а»; каждую выписанную цепь рассматривают в сочетании с каждым урезанным сечением. Для них определяют входные наборы, на которых они одновременно существу­ют; проверяющую функцию φ⁰ находят как объединение всех входных наборов.

Алгоритм вычисления проверяющей функции для короткого замы­кания (φ¹) аналогичен, только термин «цепь» необходимо заменить на термин «сечение».

Определим проверяющую функцию φ⁰_a для контакта «а»:

Контакт «а» входит в цепь G₂= a∙c₁, а также в сечения H₂= 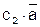и Н₃= 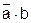. Сечения, урезанные на контакте «а» — H₂/a=с₂ и Н₃/а=b.

Цепь G₂ существует при подаче входных переменных a=1, с=1, а сечение H₂/a — при подаче с=1, т.е. цепь G2 и сечение H₂/a одновременно существуют на наборах a=1, b=1, c=1 и a=1, b=0, c=1.

Цепь G₂ существует при подаче входных переменных a=1, с=1, а сечение H₃/a — при подаче b=1, т.е. цепь G₂ и сечение H₂/a одновременно существуют на наборе a=1, b=1, c=1.

Проверяющая функция φ⁰_a= .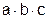

Определим проверяющую функцию φ¹_a для контакта «а»:

Контакт «а» входит в сечения H₂= 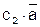и Н₃= 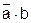, а также в цепь G₂=a∙c₁. Цепь, урезанная на контакте «а» — G₂/a=с₁.

Сечение Н₂ и цепь G₂/a одновременно существуют на наборах a=0, b=1, c=1 и a=0, b=0, c=1.

Сечение Н₃ и цепь G₂/a одновременно существуют на наборе a=0, b=1, c=1.

Проверяющая функция φ¹_a= .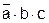

Определим проверяющую функцию φ⁰_b для контакта «b»:

Контакт «b» входит в цепь G₁= 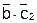и сечения H₁= 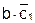и Н₃= 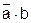. Сечения, урезанные на контакте «b» — Н₁/b= 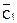и Н₃/b= .

Цепь G₁ и сечения Н₁/b= 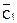и Н₃/b= одновременно существуют на наборе a=0, b=0, c=0.

Проверяющая функция φ⁰_b= .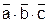

Определим проверяющую функцию φ¹_b для контакта «b»:

Контакт «b» входит в сечения H₁= 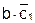и Н₃= 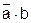и цепь G₁= 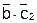. Цепь, урезанная на контакте «b» — G₁/b= .

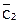Сечения H₁= 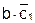и Н₃= 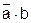и цепь G₁/b= 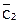одновременно существуют на наборе a=0, b=1, c=0.

Проверяющая функция φ¹_b= .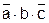

Определим проверяющую функцию φ⁰_c1 для контакта «c₁»:

Контакт «с₁» входит в цепь G₂=a∙c₁ и сечение H₁= 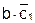. Сечение, урезанное на контакте «с₁» — H₂/с₁=b.

Цепь G₂=a∙c₁ и сечение H₂/с₁=b одновременно существуют на наборе a=1, b=1, c=1.

Проверяющая функция φ⁰_с1= .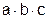

Определим проверяющую функцию φ¹_c1 для контакта «c₁»:

Контакт «с₁» входит в сечение H₁= 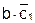и цепь G₂=a∙c₁. Цепь, урезанная на контакте «с₁» — G₂/c₁=a.

Сечение H₁= 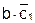и цепь G₂/c₁=a одновременно существуют на наборе a=1, b=1, c=0.

Проверяющая функция φ¹_с1= .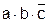

Определим проверяющую функцию φ⁰_c2 для контакта «c₂»:

Контакт «с₂» входит в цепь G₁= 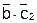и сечение H₂= 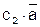. Сечение, урезанное на контакте «с₂» — Н₂/с₂= .

Цепь G₁= 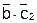и сечение Н₂/с₂= одновременно существуют на наборе a=0, b=0, c=0.

Проверяющая функция φ⁰_c2= .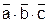

Определим проверяющую функцию φ¹_c2 для контакта «c₂»:

Контакт «с2» входит в сечение H₂= 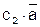и цепь G₁= 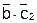. Цепь, урезанная на контакте «с2» — G₁/c₂= .

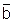Сечение H₂= 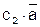и цепь G₁/c₂= 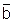одновременно существуют на наборе a=0, b=0, c=1.

Проверяющая функция φ¹_с2= .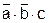

Определяем проверяющий тест, который находится как логическое произведение проверяющих функций:

Т_п= φ⁰_a∙ φ¹_a∙ φ⁰_b ∙ φ¹_b ∙ φ⁰_с1∙ φ¹_с1∙ φ⁰_c2∙ φ¹_с2 (2.18)

Подставим полученные значения проверяющих функций в выражение 2.18 и произведем его минимизацию:

Т_п= ∙ ∙ ∙ ∙ ∙ ∙ ∙ =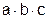

= ∙ ∙ ∙

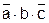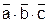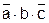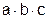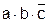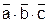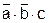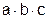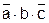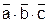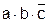
Таким образом, проверочный тест для представленной на рисунке 2.5 релейно-контактной схемы будет представлять множество входных наборов:

Т_п={ 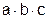, , 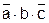, 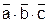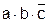} (2.19)

Дата добавления: 2015-06-28