Построение проверяющего теста. Задана функция алгебры логики (ФАЛ):

Задана функция алгебры логики (ФАЛ):

F={0, 4, 5, 7} a, b, c

Минимизируем заданную ФАЛ с помощью карты Карно и построим релейно-контактную схему для функции:

F={000, 100, 101, 111} a, b, c

Рисунок 2.3 — Карта Карно функции F={000, 100, 101, 111} a, b, c

В результате получаем минимизированную функцию:

F= (2.14)

Комбинационная релейно-контактная схема, соответствующая полученной ФАЛ, представлена на рисунке 2.4. Она содержит три входных реле — А, В и С и четыре контакта — a, b, c₁ и с₂.

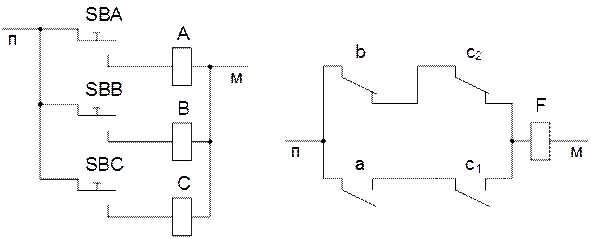
Рисунок 2.4 — Комбинационная релейно-контактная схема

Общее число проверок для схемы с m входами равно 2m. Рассмотрим только одиночные неисправности контактов. Для построения тестов релейно-контактной схемы будем использовать ТФН.

Рассматриваемая схема имеет восемь проверок, одно исправное и восемь неисправных состояний.

Функции неисправностей могут быть рассчитаны двумя методами. При первом методе неисправность вносят в схему и по полученной структуре схемы определяют искомую функцию. Схема с внесенной неисправностью, например коротким замыканием контакта а, реализует функцию f₁= . Второй метод использует влияние неисправности на формулу, отражающую структуру схемы. Между ее буквами и контактами схемы существует взаимно однозначное взаимодействие. Короткое замыкание контакта соответствует переводу соответствующей буквы в единицу, а разрыв контакта — в нуль. Для короткого замыкания контакта a функция будет иметь вид f₁= , а для обрыва — f₂= .

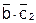В соответствии с рассмотренными методами определения функции неисправностей контактов схемы они имеют вид:

f₁=

f₂=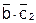

f₃=

f₄=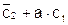

f₅=

f₆=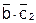

f₇=

f₈=

Для заданной релейно-контактной схемы ТФН представлена в таблице 2.6.

Таблица 2.6 — Таблица функций неисправностей

Входной набор

F

f1

f2

f3

f4

f5

f6

f7

f8

при внесении неисправности

№

a

b

c

a^1

a^0

b^1

b^0

c1^1

c1^0

c2^1

c2^0

На основании ТФН и в соответствии с выражением 2.1 для вычисления проверяющей функции находим проверяющие функции:

φ₁=1v3

φ₂=5v7

φ₃=0v4

φ₄=2v6

φ₅=6

φ₆=5v7

φ₇=0v4

φ₈=1

Проверяющий тест в соответствии с выражением 2.2 равен:

Т_п= φ₁∙ φ₂∙ φ₃∙ φ₄∙ φ₅∙ φ₆∙ φ₇∙ φ₈=

=(1v3)∙(5v7)∙(0v4)∙(2v6)∙6∙(5v7)∙(0v4)∙1=(5v7)∙(0v4)∙6∙1=

=0∙1∙5∙6v0∙1∙6∙7v1∙4∙5∙6v1∙4∙6∙7 (2.15)

Это выражение содержит четыре минимальных теста:

Т_п1=0∙1∙5∙6

Т_п2=0∙1∙6∙7

Т_п3=1∙4∙5∙6

Т_п4=1∙4∙6∙7

Дата добавления: 2015-06-28