Построение проверяющего теста

Рассмотрим построение проверяющего теста комбинационной схемы относительно константных неисправностей. Для этого по заданной ФАЛ вы­черчиваем схему с указанием всех логических элементов и связей между ни­ми. Комбинационная схема реализует функцию F = .

При этом на схеме укажем компоненты и все неисправности компо­нент. Под компонентами понимают входы и выходы элементов, и входы схе­мы. Входы схемы, выходы элементов, если они соединены с входом только одного элемента, рассматривают как одну компоненту. Если в схеме имеется точка разветвления, то в качестве компонент считаются как точки разветвле­ния, так и все ветви разветвления.

Для каждой компоненты наносим две константные неисправности К→1, К→0.

Данная схема имеет 10 компонент и 20 неисправностей. На каждый логический элемент наносим графы эквивалентных неисправностей и отношения импликации между неисправ­ностями, т.е. устанавливаем отношения между всеми неис­правностями схемы.

Затем нумеруем неисправности, при этом среди эквивалентных неис­правностей нумеруем только одну, ближе всех расположенную к выходу. Все неисправности, к которым направлены дуги, не нумеруют, а если дуга на­правлена к одной из эквивалентных неисправностей, то ни одну из них не нумеруют.

В результате выполнения данной операции сокращаем список неис­правностей, которые рассматриваем при построении теста. В данной схеме пронумеровано 8 неисправностей, в то время как исходное множество со­держит 20 неисправностей.

Рисунок 2.8 — Комбинационная схема, реализующая функцию

F =

Составляем ТФН, в которую включаем все пронумерованные неис­правности. ТФН для рассматриваемого примера, вычисленная по приведен­ным ниже функциям неисправностей, приведена в таблице 2.10. Функции неис­правностей рассчитывают методами, которые используются для релейно-контактных схем.

f₁=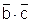

f₂=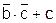

f₃=

f₄=

f₅=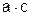

f₆=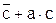

f₇=

f₈=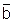

Таблица 2.10 — Таблица функций неисправностей

№

Входной набор

F

Функция неисправности

a

b

c

f1

f2

f3

f4

f5

f6

f7

f8

Вычисляем проверяющие функции в соответствии с выражением 2.1:

φ₁=5v7

φ₂=1v3

φ₃=6

φ₄=1

φ₅=0v4

φ₆=2v6

φ₇=0v6

φ₈=1v7

Затем, в соответствии с выражением 2.2, вычислим проверяющий тест:

Т_п= φ₁∙ φ₂∙ φ₃∙ φ₄∙ φ₅∙ φ₆∙ φ₇∙ φ₈

Подставим в выражение для проверяющего теста полученные проверочные функции и минимизируем получившееся выражение:

Т_п=(5v7)∙(1v3)∙6∙1∙(0v4)∙(2v6)∙(0v6)∙(1v7)=

=1∙6∙(5v7)∙(0v4)

В результате получаем четыре минимальных теста:

Т_п1=0∙1∙5∙6

Т_п2=0∙1∙6∙7

Т_п3=1∙4∙5∙6

Т_п4=1∙4∙6∙7

Дата добавления: 2015-06-28