Структурный анализ механизма

Определение недостающих размеров

1.1 Определяем длину кривошипа

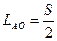(1)

где S – максимальный ход ползуна, м;

S=0,83м /с.2/

1.2 Определяем длину шатуна

(2)

где l - отношение длины кривошипа к длине шатуна

l=0,22

Для этого чертим, данный механизм и проставляем на нем все подвижные звенья, а заглавными буквами латинского алфавита обозначаем все кинематические пары и класс кинематической пары.

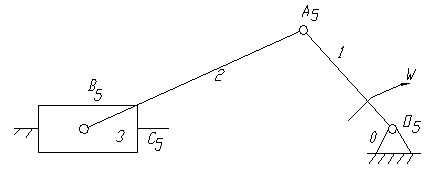рисунок 1

1 – кривошип;

2 – шатун;

3 – ползун;

О₅ – кинематическая пара пятого класса, низшая;

А₅ - кинематическая пара пятого класса, низшая;

В₅ - кинематическая пара пятого класса, низшая;

С₅ - кинематическая пара пятого класса, низшая.

2.1 Определяем степень подвижности механизма

/1 / (3)

где n – число подвижных звеньев;

р₅ – число кинематических пар пятого класса

р₄ - число кинематических пар четвертого класса

n=3

р₅=4

р₄=0

Лишних степеней свободы, высших кинематических пар, пассивных связей в механизме нет.

2.2 Отсоединяем от механизма группу Ассура второго класса

При этом оставшийся механизм должен продолжать работать, а степень подвижности его не меняется.

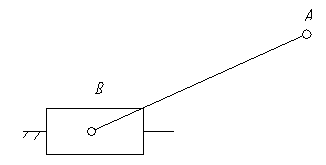Рисунок 2 – группа Ассура 2-го класса

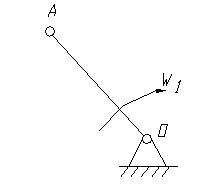2.2.1 Проверяем степень подвижности оставшегося механизма

Рисунок 3 - оставшейся механизм

где n=3

р₅=4

Класс механизма второй, так как отсоединенная группа Ассура второго класса, второй группы, второго порядка.

3 Первая задача кинематического анализа

3.1 Выбираем масштаб схемы механизма

Масштаб должен быть таким, чтобы длины всех отрезков вошли на чертеж. Он должен браться из стандартного ряда.

(5)

где AB – отрезок длинны шатуна на плане скоростей, мм

AB=188,5мм /с.4/

L_AB=1,885м

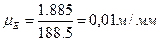
3.2 Определяем размеры кривошипа на чертеже

где L_AO=0.415м /с.4/

Строим восемь положений механизма.

Для этого на ватмане чертим две оси. На пересечении их устанавливаем циркуль, размер которого равен длине кривошипа на чертеже, и проводим окружность. Данную окружность разбиваем на восемь равных частей(угол деления равен 45⁰). Полученные линии будут являться положениями кривошипа (Рисунок 4).

Рисунок 4 – положения кривошипа

В каждое положение кривошипа устанавливаем циркуль, размер которого равен размеру шатуна на чертеже, и проводим им так, чтобы окружность пересеклась с горизонтальной осью. Эти пересечения и будут являться положениями шатуна. Соединяем линиями соответствующие положения шатуна и кривошипа (Рисунок 5).

Рисунок 5 - первое положение механизма.

4 Вторая задача кинематического анализа

4.1 Определяем скорость ведущего звена

Скорость звена всегда перпендикулярна данному звену и направлена в ту же сторону, что и угловая скорость данного звена.

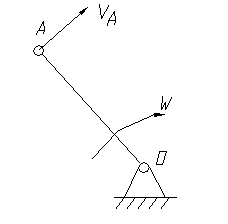рисунок 6 – скорость ведущего звена

(6)

где W₁ – угловая скорость ведущего звена, с^-1

(7)

где n – частота вращения кривошипа, об/мин

n=2250об/мин /с.2/

L_AO – 0,415м /с.4/

4.2 Определяем масштаб плана скоростей

(8)

где V’_A – отрезок скорости ведущего звена на плане скоростей, мм

V’_A=97,72мм

4.3 Определяем скорость группы Ассура для каждого положения

Рисунок 7 – направление скоростей

(9)

где V_BAx – скорость шатуна в х - положении.

Строим восемь планов скоростей.

Для этого на ватмане берем произвольную точку (полюс). Переносим параллельно (в заданном положении механизма) вектор скорости V_A, через данную точку. Из полюса откладываем его длину в масштабе на плане cкоростей (рисунок 8).

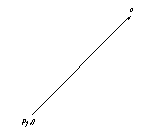Рисунок 8 – направление скорости ведущего звена

В конец вектора V_а параллельно переносим вектор V_ВА, но направление его мы не знаем. Поэтому проводим его как в одну, так и в другую сторону относительно конца вектора V_а (рисунок 9).

Рисунок 9

Так же параллельно переносим вектор V_B в полюс, но направление мы также не знаем. Поэтому проводим его как в одну, так и в другую сторону. Пересечение векторов V_B и V_а даст нам их длины. Указываем направление векторов V_B и V_а согласно уравнению (9). Для нахождения скорости средней точки шатуна S₂ нужно провести вектор из полюса к середине участка ab (рисунок 10).

Рисунок 10

Длина каждого вектора является скоростью для каждого звена.

4.3.1 Определяем скорость ползуна в каждом положении

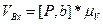(10)

где [P, b]_x – длина отрезка P, b для х – положения, мм

m_V=1м/с/мм /с.9/

4.3.2 Определяем скорость шатуна в каждом положении

(11)

[a, b]_x – длина отрезка a, b для х – положения, мм

4.3.3 Определяем скорость в точке S₂ в каждом положении

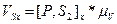(12)

[P, S₂]_x – длина отрезка P, S₂ для х – положения, мм

Числовые значения длин отрезков и скоростей приведены в таблице 1

Таблица 1

№ положения	[P,b], мм	VB, м/с	[а,b], мм	VBA, м/с	[P,S2], мм	VS, м/с
	80,03	80,03	69,95	69,95	82,18	82,18
	97,72	97,72			97,72	97,72
	58,17	58,17	69,95	69,95	72,4	72,4
			97,72	97,72	48,86	48,86
	58,17	58,17	69,95	69,95	72,4	72,4
	97,72	97,72			97,72	97,72
	80,03	80,03	69,95	69,95	82,18	82,18
			97,72	97,72	48,86	48,86

4.4 Определяем угловую скорость для шатуна в каждом положении

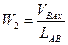(13)

где V_Bax – скорость шатуна в х – положении, м/с

L_АВ=1,885м

Числовые значения угловых скоростей приведены в таблице 2

Таблица 2

VBA, м/с	69,95		69,95	97,72	69,95		69,95	97,72
W2, с^-1	37,1		37,1	51,8	37,1		37,1	51,8

5 Третья задача кинематического анализа механизма

Относительное ускорение состоит из нормальной и тангенциальной составляющей. Нормальная составляющая относительного ускорения всегда направлена к центру вращения. Тангенциальная составляющая относительного ускорения направлена перпендикулярно звену в сторону углового ускорения.

5.1 Определяем ускорение для ведущего звена

рисунок 11

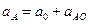(14)

где а₀ – ускорение в точке 0, м/с²

а_АО – ускорение звена АО, м/с²

а₀=0

(15)

где аⁿ_АО – нормальная составляющая ускорения а_АО, м/с²

а^t_АО – тангенциальная составляющая ускорения а_АО, м/с²

так как W₁=const, то а^t_АО=0

(16)

W₁=235.5c^-1 /с.9/

L_AB=0.415м /с.4/

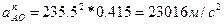
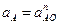
5.2 Определяем ускорение для группы Ассура в каждом положение

Рисунок 12

(17)

где а_ВАх – ускорение звена ВА, м/с²

(18)

(19)

где аⁿ_BA – нормальная составляющая ускорения а_BA, м/с²

а^t_BA – тангенциальная составляющая ускорения а_BA, м/с²

(20)

где W_2х – угловая скорость шатуна, с^-1 /с.13, табл.2/

L_AB=1.885м

Числовые значения приведены в таблице 3

Таблица 3

W2, с^-1	37.1		37.1	51.8	37.1		37.1	51.8
а^nBA, м/с

5.3 Определяем масштаб плана ускорения

(21)

где а’_А – отрезок ускорения ведущего звена на плане ускорения в 1, 3, 5, 7 положениях мм

а’_А=115,08мм

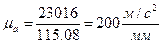
5.4 Определяем размер отрезка нормальной составляющей ускорения аⁿ_ВА в 1, 3, 5, 7, положениях на плане ускорения

(22)

где аⁿ_ВА=2596м/с² /с.15, табл.3/

5.5 Определяем размер отрезка нормальной составляющей ускорения аⁿ_ВА в 4,8 положениях на плане ускорения

аⁿ_ВА=5058м/с²

Отрезок аⁿ_ВА во 2 и 6 положениях равен нулю.

Строим восемь планов ускорения.

Принцип построения плана ускорений такой же, как и у плана скоростей.

На ватмане берем любую точку (полюс). В начале переносим параллельно (в заданном положении механизма) вектор а_А через эту точку. Откладываем его длину в масштабе от полюса. В конец вектора а_А параллельно переносим вектор аⁿ_ВА. Откладываем его длину в масштабе от конца вектора а_А (Рисунок 13).

Рисунок 13

В конец вектора аⁿ_ВА переносим параллельно вектор а^t_ВА, но направление мы не знаем. Поэтому проводим этот вектор в обе стороны относительно конца вектора аⁿ_ВА. В полюсную точку переносим параллельно вектор а_В, но направление его мы также не знаем. Поэтому проводим этот вектор в обе стороны относительно полюса. Пересечение векторов аⁿ_ВА и а_В дадут нам их длины. Указываем направление аⁿ_ВА и а_В согласно уравнению. Для нахождения ускорения средней точки Шатуна S₂ нужно соединить точки a и b прямой линией и направить вектор ускорения из полюса к середине прямой ab. (рисунок 14).

Отрезок аⁿ_ВА во 2 и 6 положениях равен нулю. Следовательно вектор а^t_ВА будет выходить из конца вектора а_А.

Рисунок 14

5.6 Определяем тангенциальное ускорение шатуна в каждом положении

(23)

где [t] – длина отрезка t для х – положения

m=200м/с²/мм /с.16/

5.7 Определяем ускорения ползуна в каждом положении

(24)

[P,b]_x – длина отрезка Pb для х – положения

5.8 Определяем ускорение в точке S₂

(25)

[P, S₂]_х – длина отрезка [P, S₂] в х – положении

Числовые значения ускорений приведены в таблице 4

Таблица 4

№ положения	[t], мм	а^tBA м/с^2	[P,b], мм	аBA, м/с^2	[P,S2]мм	aS2 м/с^2
	80,33		81,69		91,12
	117,97		25,97		58,99
	80,33		81,05		90,74
			89,79		102,3
	80,33		81,05		90,74
	117,97		25,97		58,99
	80,33		81,69		91,12
			89,79		102,3

5.9 Определяем угловые ускорения для каждого положения

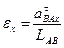(26)

а^t_ВАх –тангенциальная составляющая ускорения в х –положении, м/с² /табл.4/

L_AB=1,885м /с.4/

Числовые значения углового ускорения приведены в таблице 5

таблице 5

а^tВА м/с^2
e, с^-2

Дата добавления: 2015-06-28