Кинематические диаграммы

Построим диаграммы перемещения, скорости, ускорения в зависимости от угла поворота кривошипа.

6.1 Выбираем масштаб угла поворота кривошипа

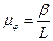(27)

где b - угол поворота за один оборот

L – длина угла поворота кривошипа на графике за один оборот, мм

b=360⁰

L=180мм

6.2 Диаграмма перемещения

6.2.1 Выбираем масштаб

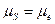(28)

где m_e=0,01м/мм /с.7/

Строим диаграмму

Примем за нулевую точк верхнее положение шатуна В₈. На ватмане нанесем оси координат. За осьY возьмем перемещение ползуна, а за Х возьмем угол поворота кривошипа. На графике длину угла поворота кривошипа разбиваем на восемь его положений (т.е. L/8). Точку пересечение осей примем за ноль.

На графике восьми положений механизма измеряем расстояние от нулевого положения механизма (В₀) до его первого положения (В₁). Это расстояние откладываем на графике от нуля по координате S. Пересечение первого положения кривошипа с первым положением шатуна даст нам искомую точку. Таким же методом строим точки для всех оставшихся положений. Так же нужно построить точки и для второго оборота кривошипа в первом и втором положениях. Затем нужно соединить эти точки, начиная с нуля (рисунок15).

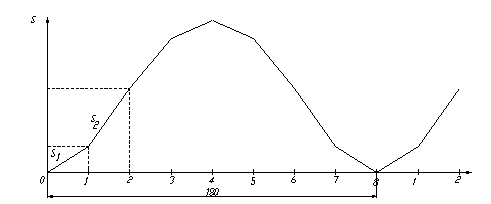Рисунок 15 – диаграмма перемещения

6.3 Диаграмма скорости

6.3.1 Определяем масштаб

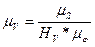(29)

где Н_V – полюсное расстояние на графике скорости, мм

Н_V=20мм

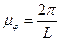(30)

L=180мм

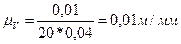
Строим график.

Для этого строим на ватмане оси координат. За осьY возьмем скорость V, а за Х возьмем угол поворота кривошипа. Откладываем полюсное расстояние H_V. Точки угла поворота кривошипа будут совпадать с первым графиком. С графика перемещения переносим параллельно линию перемещений (S₁) в полюсную точку (O_V). Продлеваем ее до пересечения с осью

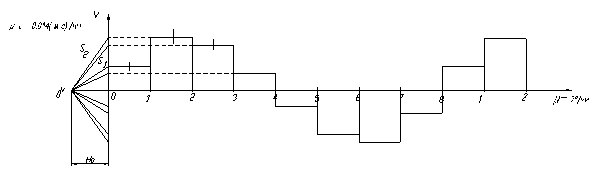V. Из полученной точки продлеваем линию параллельно оси j до пересечения с первым положением кривошипа. Полученый участок 01 разобьем пополам. Аналогично поступаем с остальными линиями (рисунок16).

Рисунок 16

Полученные середины участков соединяем кривой линией по лекалу, начиная с нулевой точки (Рисунок17).

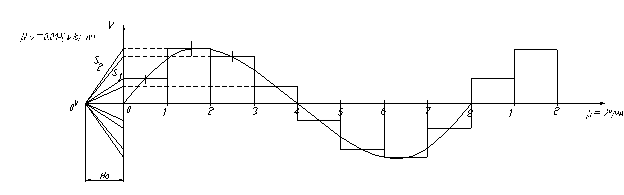
Рисунок 17

Кривую линию заменяем прямыми. То есть, начиная из нулевого положения, проводим линию до пересечения кривой линии и первого положения кривошипа на участке 01. На участке 12 проводим линию от пересечения первого положения кривошипа с кривой линией до пересечения кривой линии со вторым положением кривошипа. Аналогично поступаем и с другими участками (рисунок 18).

Рисунок 18 – диаграмма скорости

6.4 Диаграмма ускорения

6.4.1 Определяем масштаб

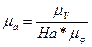(31)

Где Н_а – полюсное расстояние на графике ускорения, мм

m_v=0,01(м/с)/мм /с.20/

Н_а=30мм

m_j=0,04 рад/м /с.20/

Строим график.

Для этого строим на ватмане оси координат. За осьY возьмем ускорение а, а за Х возьмем угол поворота кривошипа. Откладываем полюсное расстояние H_а. Точки угла поворота кривошипа будут совпадать с первым графиком. Данный график строится аналогично графику скорости, но линии переносим в полюсную точку со второго графика. Построение кривой начинается не с нулевой точки, а с середины участка 12 (Рисунок 19).

Рисунок 19

Полученная кривая на участке 82 будет соответствовать кривой 02. Поэтому мы эту кривую и переносим на участок 02.

Кривую заменяем прямыми аналогично как при построении второго графика (Рисунок 20)

Рисунок 20

7 Определение реакций опор для группы Ассура

Рисунок 21 – действие сил в заданном положение механизма для расчета

Для построения всех сил нужно знать что:

- силы инерции Р_i всегда направлены в противоположную сторону ускорению центра масс звена;

- момент инерции направлен в противоположную сторону угловому ускорению звена, для заданного положения механизма;

- сила прессования направлена в противоположную сторону рабочему ходу механизма;

- силы тяжести направлены вниз;

- сила R₀₃,с которой действует стойка на ползун направлена вверх;

- направления тангенциальной и нормальной составляющей силы с которой действует кривошип на шатун, мы не знаем, поэтому первоначально их направляем в любом направлении.

7.1Определяем силу тяжести шатуна

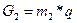(32)

где m₂ – масса шатуна, кг

q – ускорение свободного падения, м/с²

m₂=1405.5кг /с.2/

q=9,81 м/с²

7.2 Определяем силу тяжести ползуна

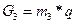(33)

где m₃ – масса ползуна, кг

m₃=2342,5кг /с.2/

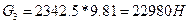
7.3 Определяем силу инерции шатуна

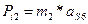(34)

где а_S6 – ускорение относительно центра масс шатуна в шестом положении

а_S6= 11798 м/с² /с.18, табл.4/

7.4 Определяем силу инерции ползуна

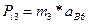(35)

где а_В6 – ускорение относительно центра масс ползуна в шестом положении

а_В6= 5194 м/с² /с.18, табл.20/

7.5 Определяем момент инерции пары сил

(36)

где e - угловое ускорение, рад/с²

J_S – момент инерции шатуна относительно оси, проходящей через центр тяжести

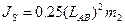(37)

L_AB=1,885м /с.4/

m₂=1405.5кг /с.2/

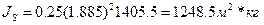
e₂=12512 /с.18, табл.18/

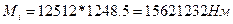
7.6 Найдем сумму всех сил относительно точки В

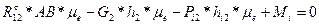(38)

где R^Т₁₂ –тангенциальная составляющая реакции, с которой действует кривошип на шатун, Н

h₂ – плечо силы тяжести относительно точки В, мм

h_i2 - плечо силы инерции относительно точки В,мм

G₂=13788 H

h₂=91,2мм

h_i2=84,47 мм

m_е=0,01м/мм /с. 5/

P_i2=16582089H /с. 25/

AB=185.5 мм /с. 4/

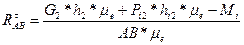(39)

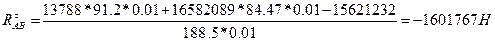
Получилось выражение со знаком «-», следовательно нужно изменить направление вектора R^Т₁₂ на противоположное.

7.7 Составим векторное уравнение

(40)

где Rⁿ₁₂ – нормальная составляющая силы, с которой действует кривошип на шатун, Н

Р_прес – сила прессования механизма, Н

R₀₃ – сила с которой действует стойка на ползун, Н

R^T₁₂=1601767H

G₂=13788 H

P_i2=16582089H /с. 25/

P_i3=12166945H /с. 25/

G₃=22980H /с.25/

P_прес=320000Н /с. 2/

7.8 Выбираем масштаб

7.9 Определяем на графике длины всех сил

(41)

где Z_x – действующая сила

m_R=110000Н/мм /с. 26/

Численные значения длин векторов сил на графике приведены в таблице 6

Таблица 6

Zx	R^T12	G2	Pi2	Pi3	G3	Pпрес
Значение, Н
N, мм		0,13	165,8	121,6	0,2	3,2

Строим график данного векторного уравнения и найдем R₀₃ и Rⁿ₁₂

На ватмане бумаги берем произвольную точку. В эту точку с заданного положения механизма для расчета переносим вектор силы R^T₁₂ в масштабе. Так как у нас векторное уравнение то остальные вектора сил переносятся так же параллельно в конец предыдущего вектора(рисунок 22).

Для нахождения вектора Rⁿ₁₂ параллельно переносим его в начальную точку и проводим до пересечения с вектором R_03. Расставляем их направления (рисунок 23).

Для нахождения силы R₁₂ надо направит вектор от начала вектора Rⁿ₁₂ к концу вектора Rⁿ₁₂. (рисунок 23)

Рисунок 22

Рисунок 23

7.10 Определяем силу, с которой действует кривошип на группу Ассура

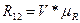(42)

где V – длина вектора R₁₂ на графике, мм

V=162,14 мм /с. 27, табл.6/

m_R=100000 Н/мм /с. 26/

Дата добавления: 2015-06-28