Определение передаточных чисел четырех типовых планетарных редукторов

10.1 Определение передаточного числа планетарного редукторов с двумя внешними зацеплениями

Рисунок 31

1 – неподвижное звено;

2, 3 – блок сателлитов;

4 – подвижное колесо;

Н – водило;

А₅ - кинематическая пара пятого класса, низшая;

D₅ - кинематическая пара пятого класса, низшая;

N₅ - кинематическая пара пятого класса, низшая;

С₄ - кинематическая пара четвертого класса, высшая;

В₄ - кинематическая пара четвертого класса, высшая;

10.1.1 Определяем степень подвижности

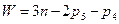(53)

где n=3

р₅=3

р₄=2

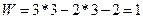
Если степень подвижности равна единицы, то данный редуктор является планетарным.

10.1.2 Определяем передаточное отношение от подвижного колеса к водилу

Верхний индекс показывает, какое звено неподвижно.

Мысленно остановить водило, и заменить неподвижное колесо подвижным. Теперь следует определять от подвижного колеса к тому колесу, которое было неподвижным. Полученный результат нужно вычесть из единицы.

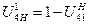(54)

где m – число внешних зацеплений;

U^H₄₁ – передаточное отношение от 4 к 1 колесу

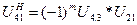(55)

где U_4.3 – передаточное отношение от 4 к 3 колесу

U₂₁ – передаточное отношение от 2 к 1 колесу

m=2

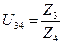(56)

где Z₃ – число зубьев третьего сателлита;

Z₄ – число зубьев подвижного колеса 4;

Z₃=19

Z₄=45

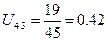
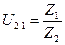(57)

где Z₁ – число зубьев неподвижного колеса 1;

Z₄ – число зубьев подвижного колеса 4;

Z₁=47

Z₂=18

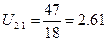
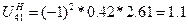
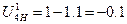
10.1.3 Определяем передаточное отношение от водила к подвижному колесу

Искомое передаточное отношение обратное передаточному отношению от подвижного колеса к водилу. Следовательно, нужно 1 поделить на передаточное отношение от подвижного колеса к водилу.

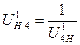(58)

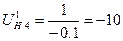
10.2 Определение передаточного числа планетарного редуктора с одним внешними и одним внутренним зацеплениями

Рисунок 32

1 – неподвижное звено;

2, 3 – блок сотилитов;

4 – подвижное колесо;

Н – водило;

А₅ - кинематическая пара пятого класса, низшая;

D₅ - кинематическая пара пятого класса, низшая;

N₅ - кинематическая пара пятого класса, низшая;

С₄ - кинематическая пара пятого класса, высшая;

В₄ - кинематическая пара пятого класса, высшая;

10.2.1 Определяем степень подвижности

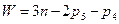
где n=3

р₅=3

р₄=2

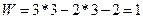
10.2.2 Определяем передаточное отношение от подвижного колеса к водилу

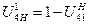(59)

где m – число внешних зацеплений;

U^H₄₁ – передаточное отношение от 4 к 1 колесу

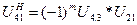(60)

где U_4.3 – передаточное отношение от 4 к 3 колесу

U₂₁ – передаточное отношение от 2 к 1 колесу

m=1

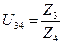(61)

где Z₃ – число зубьев третьего сателлита;

Z₄ – число зубьев подвижного колеса 4;

Z₃=19

Z₄=45

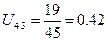
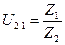(62)

где Z₁ – число зубьев неподвижного колеса 1;

Z₄ – число зубьев подвижного колеса 4;

Z₁=47

Z₂=18

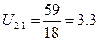
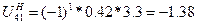
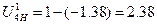
10.2.2 Определяем передаточное отношение от водила к подвижному колесу

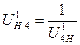(63)

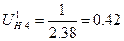
10.3 Определение передаточного числа планетарного редукторов с двумя внутренним зацеплениями

Рисунок 33

1 – неподвижное звено;

2, 3 – блок сателлитов;

4 – подвижное колесо;

Н – водило;

А₅ - кинематическая пара пятого класса, низшая;

D₅ - кинематическая пара пятого класса, низшая;

N₅ - кинематическая пара пятого класса, низшая;

С₄ - кинематическая пара четвертого класса, высшая;

В₄ - кинематическая пара четвертого класса, высшая;

10.3.1 Определяем степень подвижности

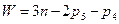
где n=3

р₅=3

р₄=2

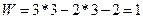
10.3.2 Определяем передаточное отношение от подвижного колеса к водилу

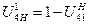(64)

где m – число внешних зацеплений;

U^H₄₁ – передаточное отношение от 4 к 1 колесу

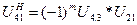(65)

где U_4.3 – передаточное отношение от 4 к 3 колесу

U₂₁ – передаточное отношение от 2 к 1 колесу

m=0

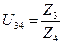(66)

где Z₃ – число зубьев третьего сателлита;

Z₄ – число зубьев подвижного колеса 4;

Z₃=18

Z₄=59

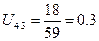
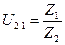(67)

где Z₁ – число зубьев неподвижного колеса 1;

Z₄ – число зубьев подвижного колеса 4;

Z₁=60

Z₂=19

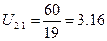
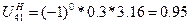
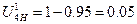
10.3.3 Определяем передаточное отношение от водила к подвижному колесу

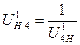(68)

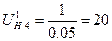
10.4 Определение передаточного числа планетарного редукторов с внутренним зацеплением и паразитным колесом

1 – неподвижное звено;

2 – сателлит;

4 – подвижное колесо;

Н – водило;

А₅ - кинематическая пара пятого класса, низшая;

D₅ - кинематическая пара пятого класса, низшая;

N₅ - кинематическая пара пятого класса, низшая;

С₄ - кинематическая пара четвертого класса, высшая;

В₄ - кинематическая пара четвертого класса, высшая;

10.4.1 Определяем степень подвижности

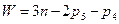
где n=3

р₅=3

р₄=2

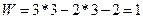
10.4.2 Определяем передаточное отношение от подвижного колеса к водилу

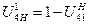(69)

где m – число внешних зацеплений;

U^H₄₁ – передаточное отношение от 4 к 1 колесу

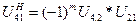(70)

где U_4.2 – передаточное отношение от 4 ко 2 колесу

U₂₁ – передаточное отношение от 2 к 1 колесу

m=1

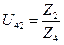(71)

где Z₂ – число зубьев сателлита;

Z₄ – число зубьев подвижного колеса 4;

Z₂=20

Z₄=25

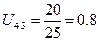
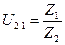(72)

где Z₁ – число зубьев неподвижного колеса 1;

Z₄ – число зубьев подвижного колеса 4;

Z₁=65

Z₂=20

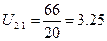
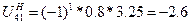
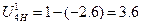
10.4.3 Определяем передаточное отношение от водила к подвижному колесу

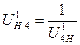(73)

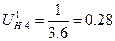
Дата добавления: 2015-06-28