Пределы применимости формулы Эйлера

Влияние способов закрепления концов стержня на критическую силу

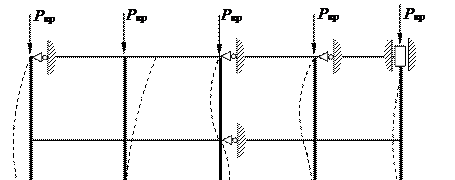
Формула Эйлера получена для случая шарнирного закрепления концов стержня, когда потеря устойчивости происходит по одной полуволне. Для других случаев закрепления формула Эйлера принимает вид (рис. 10.7):

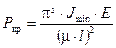, (10.4)

где μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.

Значение коэффициента μ с достаточной для расчетной практики точностью может быть вычислено по формуле:

,

где s – количество полуволн по которым происходит потеря устойчивости при данном способе закрепления концов стержня.

Получив значение критической силы, мы можем найти и значение критического напряжения s_кр, разделив критическую силу Р _кр на площадь сечения:

.

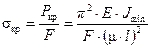Учитывая, что отношение равно квадрату минимального радиуса инерции поперечного сечения , получим:

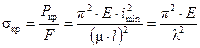, (10.5)

где l - безразмерный коэффициент называемый гибкостью стержня:

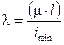, (10.6)

Полученная зависимость (10.5) представляет собой гиперболическую кривую, называемую гиперболой Эйлера.

В качестве примера на рисунке 10.8 приведена гипербола Эйлера для стали марки Ст3, для которой модуль упругости Е = 2,1×10⁵ МПа. Из графика видно, что при возрастании гибкости стержня критическое напряжение стремиться к нулю и, наоборот, по мере приближения гибкости к нулю критическое напряжение увеличивается.

Однако вывод формулы Эйлера был построен на предположении, что напряжения в стержне не превышают предела пропорциональности:

,

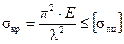откуда предельное значение гибкости:

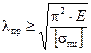. (10.7)

Значит формула Эйлера непригодна для стержней с гибкостью меньшей l_пр. Например, для стали марки Ст3 формула Эйлера становится непригодной, если:

.

То же значение можно получить, рассматривая график гиперболы Эйлера (рис. 10.8).

Потеря устойчивости может происходить и при напряжениях, превышающих предел пропорциональности. Опытным путем было установлено, что для стержней с гибкостью меньше l_пр действительные критические напряжения ниже критических напряжений, определенных по формуле Эйлера. Поэтому использование формулы Эйлера для стержней, теряющих устойчивость за пределом пропорциональности, не только принципиально неправильно, но и крайне опасно.

Что бы определить значения критических напряжений для стержней с гибкостью меньше l_пр проводились многочисленные испытания. На основании результатов экспериментальных исследований Ф. Ясинский предложил эмпирическую формулу, показывающую, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:

, (10.8)

где a и b - величины, зависящие от материала; их значения приводятся в справочниках.

Например, для стали марки Ст3 значения данных коэффициентов составляют а = 310 МПа; b = 1,14 МПа.

На рис. 10.9 пунктиром показана прямая, уравнение которой соответствует выражению (10.8). Очевидно, что с правой стороны данная прямая ограничивается гиперболой Эйлера.

При некотором значении гибкости (обозначим его l₀) величина s_кр становиться равной предельному напряжению при сжатии: s⁰ = s_т - для пластичных материалов или s⁰ = s_в - для хрупких материалов. Стержни, у которых l < l₀, называют стержни малой гибкости. Их рассчитывают только на прочность.

Таким образом, для стали марки Ст3 график s_кр = f (l)состоит из трех частей: гиперболы Эйлера при l > 100, наклонной прямой при 60 < l < 100 и горизонтальной прямой при l < 60. Горизонтальная прямая соответствует пределу текучести.

Дата добавления: 2015-06-28