Понятие о динамическом действии нагрузки

Лекция 11 Динамическое нагружение

Вопросы для самопроверки

1. Опишите явление потери устойчивости.

2. Какая механическая система называется устойчивой и неустойчивой?

3. Приведите примеры устойчивых и неустойчивых объектов.

4. Что означает выражение «сжатый стержень потерял устойчивость»?

5. Какая сила называется критической?

6. Почему в реальных конструкциях сжимающие стержень силы должны быть меньше критических?

7. Почему нельзя допускать потерю устойчивости элементов конструкций?

8. Запишите формулу Эйлера.

9. Как влияют условия закрепления стержня на величину критической силы?

10. Сформулируйте условие применимости формулы Эйлера.

11. Запишите формулу Ясинского.

12. Могут ли быть такие случаи, когда сжатый стержень не будет терять устойчивость?

13. Нарисуйте график зависимости s_кр = f (l).

14. Опишите в общем виде схему расчета сжатых стержней с помощью коэффициента уменьшения допускаемого напряжения.

Понятие о динамическом действии нагрузки; удар; механические свойства материалов при ударе; напряжения, изменяющиеся во времени; явление усталости материалов; влияние конструктивно-технологических факторов на предел усталости; практические меры повышения сопротивления усталости

Ранее во всех рассмотренных нами задачах предполагалось, что действующие нагрузки статические, т.е. не изменяющиеся с течением времени. При проектировании машин обычно сталкиваются с деталями, находящимися в неравномерном движении, что приводит к появлению инерционных нагрузок.

Примером статической нагрузки, или статического действия нагрузки, может послужить действие подвешенного на цепи груза. Это действие остается статическим, если груз будет подниматься цепью с постоянной скоростью. Но тот же груз, поднимаемый цепью с ускорением, будет действовать на цепь динамически. Для расчета цепи в данном случае мы должны учесть не только вес груза, но и силу инерции груза.

Для примера рассмотрим расчет равномерно вращающегося тонкого кольца (рис. 11.1, a).

Для расчета примем следующие обозначения: r - средний радиус кольца; F - площадь поперечного сечения; g - удельный вес материала; w - угловая скорость кольца; g - ускорение силы тяжести.

Рассмотрим бесконечно малый элемент кольца массой dm, вырезанный двумя плоскостями, составляющими центральный угол d j (рис. 11.1, б)

Элементарная сила инерции dФ:

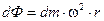. (11.1)

Элементарная масса, выраженная через площадь сечения кольца:

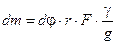. (11.2)

Элементарная сила инерции с учетом (11.2) будет равна:

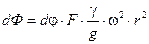. (11.3)

Для определения продольной силы N в поперечном сечении кольца рассмотрим равновесие половины кольца под действием двух продольных сил N и суммы вертикальных составляющих элементарных сил инерций:

,

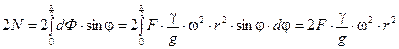откуда

. (11.4)

Полагая, что в тонком кольце все волокна растягиваются одинаково, найдем напряжение в сечении кольца:

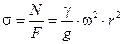. (11.5)

Определим теперь, на сколько удлинится радиус вращающегося кольца. Относительное удлинение волокон кольца равны:

.

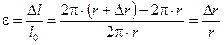Из закона Гука:

.

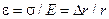Откуда

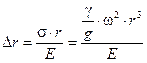. (11.6)

Дата добавления: 2015-06-28