Механические свойства материалов при ударе

Удар

К динамическому виду нагрузки относится так же ударная нагрузка. С явлением удара приходиться иметь дело, когда скорость рассматриваемого элемента конструкции или соприкасающихся с ним частей в очень короткий промежуток времени изменяется на конечную величину. Определение силы удара весьма затруднительно, так как неизвестно время соударения, поэтому в инженерной практике обычно пользуются энергетическим методом. В качестве примера рассмотрим систему с одной степенью свободы (рис. 11.2,а), которая представляет собой пружину с коэффициентом жесткости с и падающий на нее груз массой m с высоты H.

Груз m при касании пружины будет обладать кинетической энергией Т, которую можно выразить через скорость V_к груза в момент касания или высоту H:

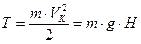. (11.7)

После того, как груз коснется пружины, он начет деформировать пружину. Когда вся кинетическая энергия груза перейдет в потенциальную энергию сжатой пружины, груз остановится (рис. 11.2, б), пружина получит свою наибольшую динамическую деформацию d_Д, а сила, сжимающая пружину, достигнет максимума. При составлении энергетического баланса здесь нужно учитывать изменение потенциальной энергии П груза на динамической деформации d_Д:

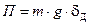. (11.8)

Упругая энергия U сжатой пружины:

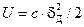. (11.9)

Составим энергетический баланс:

,

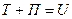или

,

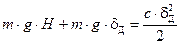который перепишем в следующем виде:

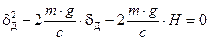. (11.10)

Рассматривая статическое равновесие упругой системы (рис. 11.2, в), отношение силы тяжести груза к жесткости пружины равно статической деформации пружины d_ст:

.

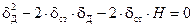Получили квадратное уравнение, из которого динамическая деформация определится как:

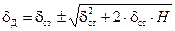. (11.11)

Поскольку знак минус в этом выражении не соответствует физической стороне рассматриваемой задачи, следует сохранить знак плюс. Запишем выражение (11.11) в виде:

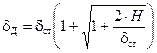. (11.12)

Величину, стоящую в скобках называют коэффициентом динамичности:

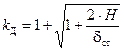. (11.13)

Коэффициент динамичности, выраженный через скорость груза в момент касания пружины с учетом выражения (11.7) будет равен:

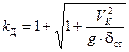. (11.14)

Окончательно динамическая деформация пружины определится как:

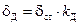. (11.15)

Динамический коэффициент показывает, во сколько раз деформация при ударе больше деформации при статическом приложении нагрузки. В том же отношении изменяются внутренние силы и напряжения:

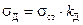. (11.16)

Из анализа выражения 11.14 видно, что коэффициент динамичности зависит от кинетической энергии падающего груза. В случае если груз опускается на упругую систему мгновенно без начальной скорости, динамическая деформация уже вдвое превышает статическую. Соответственно в два раза большими оказываются и напряжения.

Коэффициент динамичности, а, следовательно, и динамические напряжения, также зависят от жестокости упругой системы. При большей жесткости статические деформации имеют меньшие значения, а динамические напряжения при этом увеличиваются. Поэтому снижение напряжений при ударе может быть достигнуто уменьшением жесткости системы.

Зависимости для определения динамических напряжений и деформаций, полученные на примере падения груза на пружину применимы и для других упругих систем (расчет на удар при растяжении – сжатии, кручении и изгибе).

В каждом случае придерживаются следующего порядка расчета:

а) в месте падения груза к упругой системе прикладывают статическую нагрузку, равную весу падающего груза;

б) определяют статическую деформацию упругой системы;

в) определяют напряжения в материале, возникающие от приложения статической нагрузки;

г) определяют коэффициент динамичности;

д) определяют динамические напряжения и деформации.

е) сравнивают напряжения при ударе с допускаемыми напряжениями:

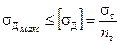. (11.17)

Обычно коэффициент запаса n _т принимают равным n _т = 2.

Полученные выше выражения получены без учета массы упругой системы, к которой прикладывается ударная нагрузка. Учет массы дает меньшие значения динамических напряжений, поэтому, рассчитывая конструкции без учета ее массы, мы получаем дополнительный запас прочности.

Для проверки способности материала сопротивляться ударным нагрузкам проводят испытания ударным изгибом – определение ударной вязкости надрезанных образцов. Эти испытания проводят на маятниковых копрах (рис. 11.3, а). На рис. 11.3, б показан применяемый при испытании образец. Разность высот маятника до и после удара позволяет вычислить работу А, израсходованную на разрушение образца.

Ударной вязкостью материала называется величина работы разрушения образца, отнесенная к площади поперечного сечения в месте надреза F:

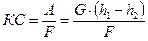. (11.18)

Данные об ударной вязкости не могут быть использованы при расчете на прочность, но они позволяют оценить особое качество металла – его склонность к хрупкости при динамических нагрузках. Низкая ударная вязкость служит основанием для браковки материала. Стали, применяемые для изготовления деталей, работающих при динамических нагрузках, должны иметь ударную вязкость не менее 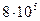¸ 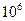Дж/м².

Дата добавления: 2015-06-28