Колебания без затухания

Свободные колебания систем с одной степенью свободы.

Элементов

Жесткость системы при последовательном соединении упругих

При последовательном соединении пружин (рис. 12.5) на каждую из них действует вес груза Q. Очевидно, что:

,

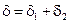или, в соответствии с формулой (12.1):

; .

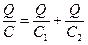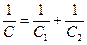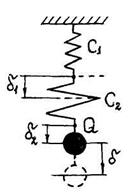
Рисунок 12.5

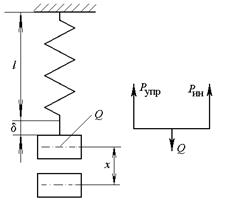
Рисунок 12.6

Окончательно имеем:

.

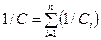Таким образом, при последовательном соединении упругих элементов величина, обратная жесткости системы, равна сумме величин, обратных жесткости упругих элементов, ее составляющих.

В данном случае и в дальнейшем ограничимся рассмотрением таких колебаний, для которых справедлив закон Гука и принцип независимости действия сил.

Рассмотрим простейшую систему, состоящую из груза, подвешенного на вертикально расположенной пружине (рис. 12.6). Влиянием собственного веса пружин пренебрегаем. Направим ось x вдоль оси пружины вниз.

За начало отсчета 0 возьмем положение статического равновесия груза Q.

В этом положении пружина растянута на величину d = Q / C, где С - жесткость пружины. Рассмотрим движение груза в произвольный момент времени t. Отклонение центра массы груза в этот момент от положения статического равновесия вниз обозначим через х. Получаем:

; ; .

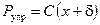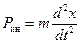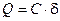При составлении уравнения движения будем исходить из принципа Даламбера, который заключается в том, что к движущейся с ускорением системе применимы соотношения статики при условии, что в число внешних сил включена фиктивная сила инерции, равная произведению массы на ускорение и направленная против ускорения. Полагаем, что скорость dx / dt и ускорение d ² x / dt ² совпадают по направлению с отклонением X. При отклонении груза возникает упругая сила Р _упр которая стремится вернуть груз в состояние равновесия и потому называется восстанавливающей силой.

Дифференциальное уравнение колебаний получим, спроектировав все действующие силы на вертикальную ось:

.

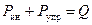Отсюда имеем:

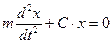, (12.3)

Или

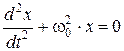, (12.4)

где .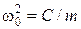

Решением уравнения (12.3) будет:

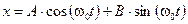. (12.5)

где А и В - постоянные интегрирования, зависящие от начальных условий, т.е. от положения груза m = Q / g и его скорости dx / dt в момент времени t = 0.

Если заданы начальная координата груза х ₀ и начальная скорость u₀, то из (12.5) определим:

; .

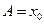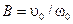Полагая

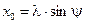и 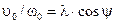, (12.6)

решение (12.5) можно представить в виде:

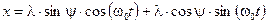. (12.7)

или

,

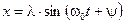где l - амплитуда колебаний, определяемая формулой:

.

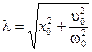Величина w₀ t + y называется фазой колебаний, а величина y - сдвигом фазы. На основании (12.7) y может быть определена из условия tgy = х ₀×w₀/u₀.

Уравнение (12.7) выражает процесс чисто периодического собственного колебания системы. График его представлен на рис. 12.7.

Период колебаний Т определяется из условия, что при увеличении времени t на величину Т аргумент, стоящий под знаком синуса, изменится на 2p:

.

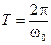Период представляет собой время, в течение которого совершается одно колебание. Если Т - время одного колебания, то в 2p секунд будет происходить w₀ колебаний. Поэтому величина w₀ и носит название круговой частоты (в отличие от секундной частоты f = 1/ Т):

.

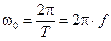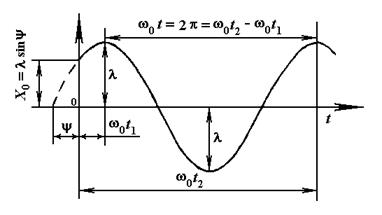
Рисунок 12.7

Круговую частоту часто называют частотой собственных колебаний системы, поскольку она, как это видно из (12.4), зависит не от начальных обстоятельств колебательного процесса, а от величины колеблющейся массы и жесткости системы. Формуле (12.4) можно придать вид:

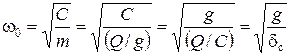, (12.8)

где g - ускорение свободного падения, м/с²; d_с - статическое удлинение пружины под действием груза Q.

Дата добавления: 2015-06-28