Расчет подачи, при которой полностью используются режущие свойства инструмента и мощность станка

Подставим выражение (4.8) и (4.24) в уравнение (4.23):

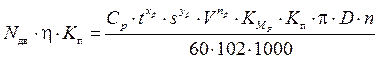. (4.25)

Решив уравнение(4.24) относительно подачи, получим

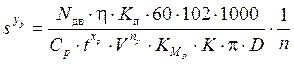. (4.26)

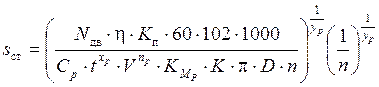. (4.27)

По уравнению (4.27) для каждого числа оборотов шпинделя мо­жет быть найдена такая подача s _ст., при которой мощность станка, будет использована полностью.

Есть такая подача, при которой полностью используются ре­жущие свойства резца и мощность станка. Такая подача называется одновременной и обозначается s _одн.

Для нахождения подачи s _одн делим уравнение (4.26) на уравнение (4.19):

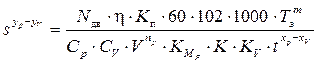. (4.28)

откуда

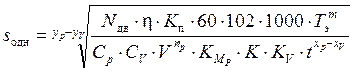. (4.29)

На двойной логарифмической сетке построим прямые линии уравнений (4.20) и (4.27), (рис. 4.4).

Точка пересечения прямых дает значения подачи и оборотов шпинделя, при которых полностью используются режущие свойства резца и мощность станка.

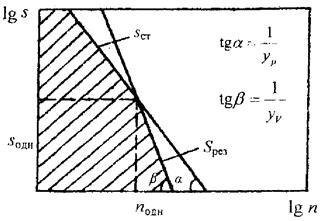
Рис. 4.4. К определению s _одн

Сравним подачи s ₀ и s _одн. Могут быть три случая:

1. s ₀ > s _одн;

2. s ₀ < s _одн;

3. s ₀ = s _одн.

Третий случай – идеальный. При третьем случае находятся обороты шпинделя n _одни подсчитывается скорость резания при этих оборотах.

Первый случай: s ₀ > s _одн.

В этом случае ограничение происходит по мощности станка. Находим обороты шпинделя n по уравнению (4.26),в которое надо подставить подачу s ₀.

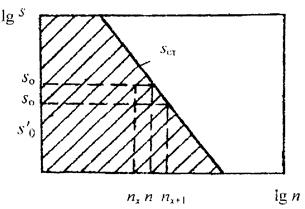
Рис. 4.5. К определению s ₀ и s' ₀

Большинство станков имеют ступенчатый ряд чисел оборотов шпинделя. Поэтому найденное расчетом число оборотов будет нахо­диться между какими-то соседними числами оборотов шпинделя n_x и n_{x +1} (рис. 4.5).

Для оборотов n_x берется подача s ₀.

Для оборотов n_{x +1} берется подача s '₀, подсчитываемая по уравнению (4.28), в которое вместо n надо подставить n_{x +1}.

Таким образом, на заданном станке можно работать на одном из двух режимов: n_x – s ₀ или n_{x +1} – s '₀. Выгоднее работать на том режиме, который обеспечит большую производительность, т.е. большую минутную подачу.

Поэтому сравниваем: ;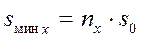

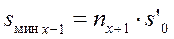. (4.30)

Выбираем ступень, при которой минутная подача больше.

Второй случай: s ₀ < s _одн.

В этом случае ограничение происходит по режущим свойствам резца. Находим обороты шпинделя n по уравнению (4.26), в которое надо подставить подачу s ₀.

Полученное расчетом число оборотов будет находиться между соседними числами оборотов шпинделя n_у и n_{у +1} (рис. 4.6).

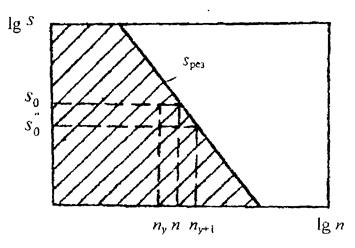
Рис. 4.6. К определению s ₀ и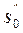

Для оборотов n_у берется подача s ₀.

Для оборотов n_{у +1} берется подача 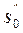, подсчитываемая уравнением (4.27), в которое вместо n надо подставить n_{у +1}.

Таким образом, на заданном станке можно работать на одном из двух режимов: n_у – s ₀ или n_{у +1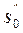} – . Выгоднее работать на том режиме, которой обеспечит большую минутную подачу.

Поэтому сравниваем: ;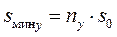

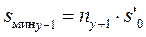. (4.31)

Выбираем ступень, у которой минутная подача больше.

Дата добавления: 2015-06-29